并查集是一种非常有用的数据结构,它的主要功能是动态加边和查询两个点的连通性。在开始学习并查集之前,可以先看看一个故事,这个故事看完了,并查集也就学的差不多了。传送门: 并查集故事
并查集的本质是维护一个森林,而森林里的每一棵树里的每一个节点都会维护它的父亲节点。
Slow Find Slow Union
想像一下,如果我们不用并查集这种数据结构,而是用普通的集合做find和union操作,会是什么情况(解释一下,find操作用来判断两者是不是在同一个集合,union操作就是将两个集合进行合并)

以上的每一个格子都表示一个集合,从操作上我们可以明显的看出,每次合并一个集合,都需要将一个集合里的元素全部移动到另一个集合中去。find操作也是很慢的,每次都需要将集合里面的一个元素和另一个集合里面的元素作比较。
有没有改进的方法呢?那当然是有的
Quick Find Slow Union
解决的方法就是使用数组下标来进行索引:
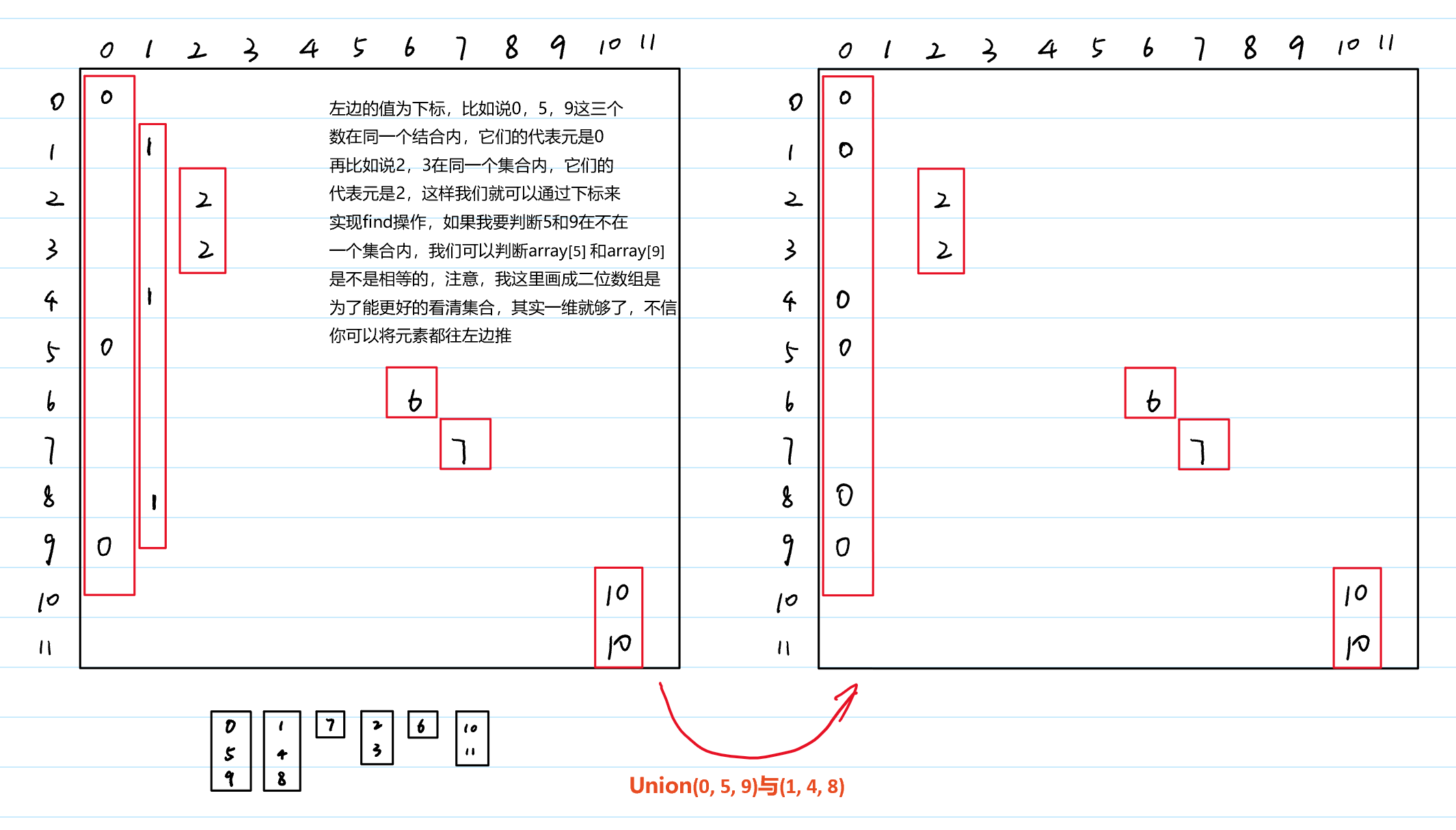
这样就可以快速实现find操作,如果你将我画的表格看成一个一维数组,就是将所有元素都往左推,那么关系:fa[A] = B 这就表示A是属于B这个集合的,而B就是代表元,也就是故事中的掌门。可以看到find操作为常数时间,但是Union操作还是很慢。
有没有改进的方法呢?那当然是有的 * 2
Mid Find Quick Union
我们将集合间的关系用数组表示之后: fa[5] = 0,说明5的爸爸是0,fa[0] = 0,说明0是这个集合的代表元。集合种元素的关系如下图,位于根节点的位置是代表元。
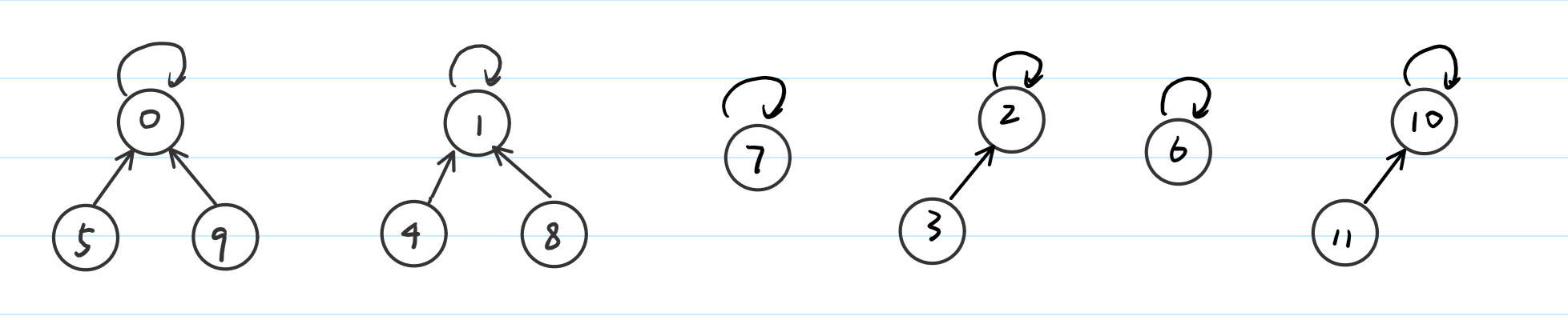
当我们要做find操作时,比如需要知道5是在哪个集合,只需要一直往上去找就好了,如果我们要做union操作:将0所代表的集合与1所代表的集合合并,我们就可以这样来操作:
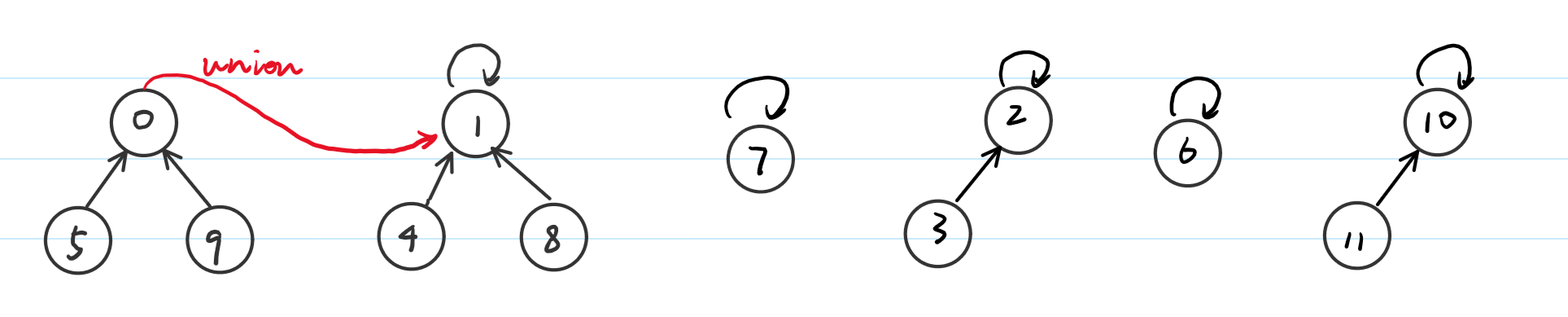
这样就将两个集合合并了。
现在,我们还有一个问题,能不能将find操作也优化一下呢?那当然是可以的的 * 3
Quick Find Quick Union
当我们在进行查询操作的时候,我们很可能遇到这样的情况:
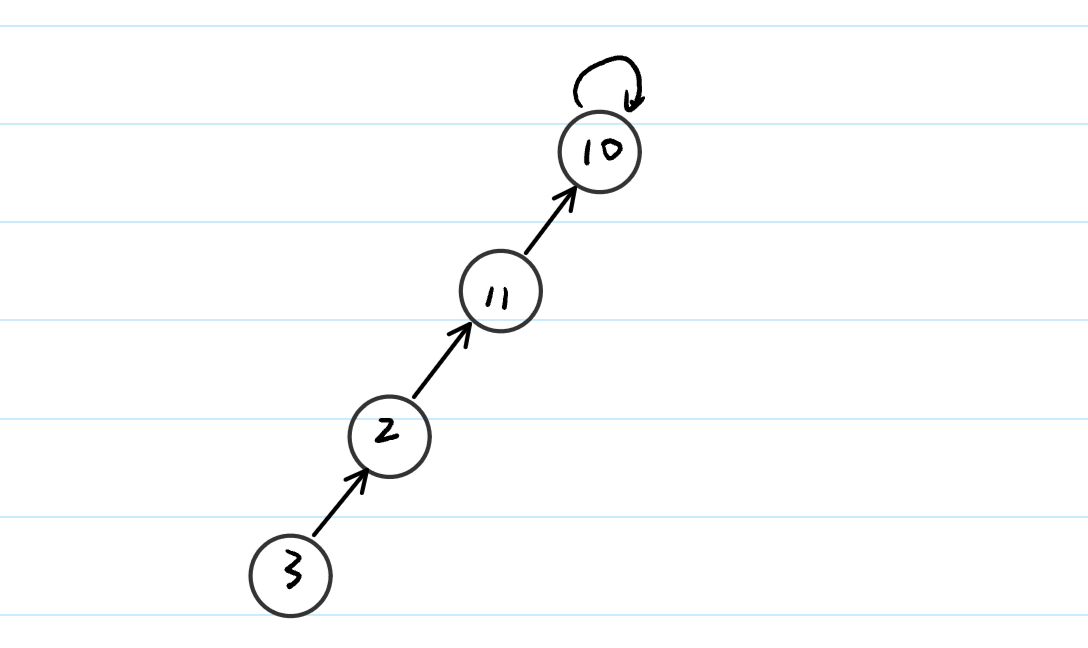
当我们要进行find(3)操作时,我们需要一步一步地往上找,这就增加了时间开销,这个时候,我们就可以使用路径压缩来进行解决。如果我们能将路径变成下图的情况,那是再好不过的:
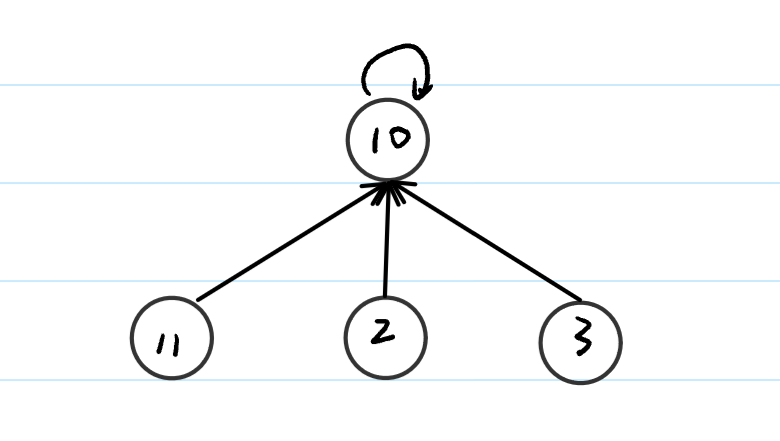
这种操作就叫做路径压缩,我们希望我们所构造的关系树时越来 越 " 矮 ",更加一般的情况:
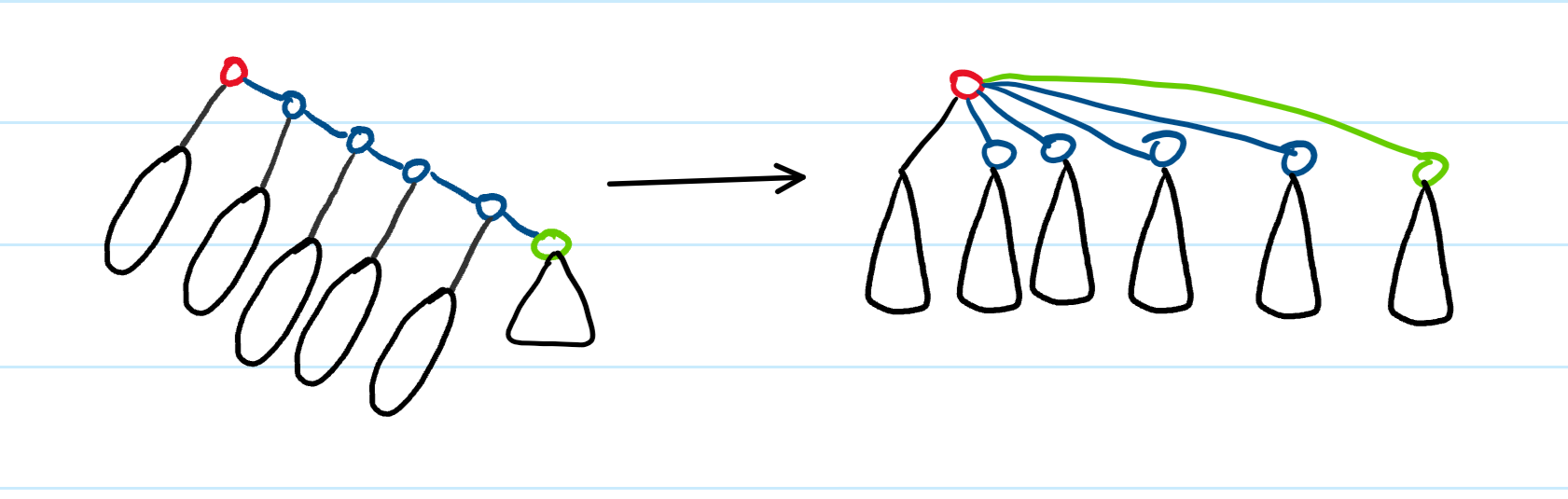
现在,我们的find操作比刚才的find要快上不少了。
代码
并查集并没有一个固定的代码模板,在题目中千变万化,了解其思想时最重要的
#include<iostream>
using namespace std;
const int MAXN = 10005;
int fa[MAXN];
int find(int x) {
while(x != fa[x])
x = fa[x];
return x;
}
void union(int x , int y) { //合并x元素和y元素的两个集合
fa[find(a)] = find(b);
}
int main(){
for(int i = 0 ; i < n ; ++i) //n为数据规模
fa[i] = i; //初始化
}
路径压缩:将x的祖先设置为x的父亲
#include<iostream>
using namespace std;
const int MAXN = 10005;
int fa[MAXN];
int find(int x) {
if(x != fa[x]) //查找的过程中就可以进行路径压缩
return fa[x] = find(fa[x]);
}
void union(int x , int y) { //合并x元素和y元素的两个集合
fa[find(a)] = find(b);
}
int main(){
for(int i = 0 ; i < n ; ++i) //n为数据规模
fa[i] = i; //初始化
}







Comments NOTHING