哈希表
题目描述:
你有一个盒子,你可以往里面放数,也可以从里面取出数。
初始时,盒子是空的,你会依次做 Q 个操作,操作分为两类:
插入操作:询问盒子中是否存在数 x,如果不存在则把数 x 丢到盒子里。
删除操作:询问盒子中是否存在数 x,如果存在则取出 x。
对于每个操作,你需要输出是否成功插入或删除。
输入
第一行一个正整数 Q,表示操作个数。
接下来 Q 行依次描述每个操作。每行 2 个用空格隔开的非负整数 op,x 描述一个操作:op 表示操作类型, op=1 则表示这是一个插入操作,op=2 则表示这是一个删除操作;x 的意义与操作类型有关,具体见题目描述。
数据范围
对于 100% 的数据,保证 x<10^18,Q≤5*10^5。
样例输入
6
1 100
1 100
2 100
1 200
2 100
2 200
样例输出
Succeeded
Failed
Succeeded
Succeeded
Failed
Succeeded
这道题的解法很多,主要涉及到插入、查询和删除操作,但需要考虑的是数据规模,第一个比较简单的方法是直接使用一个容器来维护这些数据,在stl里面,这个操作最快的是set,如果不清楚set是啥,可以在我的博客里面搜一下。set的底层是基于红黑树实现的,这种数据结构非常高级,插入查询和删除都能在O(logn)的时间内完成。下面是代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//使用查询和插入速度很快的数据结构
set <ll> container;
bool check(int op, ll x) {
if(op == 1){ //如果容器里面没有,插入
if(container.find(x) == container.end()){
container.insert(x);
return true;
}
else
return false;
}
else //如果容器里面有,删除
if(container.find(x) != container.end()) {
container.erase(x);
return true;
} else
return false;
}
int main() {
int Q, op;
ll x;
scanf("%d", &Q);
while (Q--) {
scanf("%d%lld", &op, &x);
puts(check(op, x) ? "Succeeded" : "Failed");
}
return 0;
}
第二种操作比较重要,使用哈希表来进行存储,哈希表我当年学习数据结构的时候并没有实现过,只是了解它的原理,但是了解原理之后,实现还是比较简单的,我这里使用的是二维数组来存储,只不过如果每一行后面有冲突需要挂元素的时候,我使用vector来存,比较节省空间。
代码如下:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int Mod = 1000003; //哈希的模长
vector <ll> table[Mod]; //哈希表,向量中每个元素都是一个table数组
int Hash(ll x) {
return x % Mod;
}
bool check(int op, ll x) {
int h = Hash(x); //找出哈希值
vector <ll> :: iterator ptr = table[h].end();
for(vector <ll> :: iterator it = table[h].begin(); it != table[h].end(); it++)
if(*it == x) { //看之前在不在vector中
ptr = it;
break;
}
if(op == 1) { //插入元素
if(ptr == table[h].end()) { //如果之前没有找到
table[h].push_back(x);
return true;
}
return false;
} else { //else在这里的功能是删去x的元素
if(ptr != table[h].end()) //指针不为表首则可以删除
{
*ptr = table[h].back();
table[h].pop_back(); //最后一个元素弹出
return true;
}
return false;
}
}
int main() {
int Q, op;
ll x;
scanf("%d", &Q);
while (Q--) {
scanf("%d%lld", &op, &x);
puts(check(op, x) ? "Succeeded" : "Failed");
}
return 0;
}
哈夫曼
题目如下:
有一篇文章,文章包含 n种单词,单词的编号从 1 至 n,第 i 种单词的出现次数为 w[i]。
现在,我们要用一个 2 进制串(即只包含 0 或 1 的串) s[i] 来替换第 i 种单词,使其满足如下要求:对于任意的 1≤i,j≤n(i≤j),都有 s[i] 不是 s[j] 的前缀。(这个要求是为了避免二义性)
你的任务是对每个单词选择合适的 s[i],使得替换后的文章总长度(定义为所有单词出现次数与替换它的二进制串的长度乘积的总和)最小。求这个最小长度。
字符串 S1(不妨假设长度为 n)被称为字符串 S2 的前缀,当且仅当:S2 的长度不小于 n,且 S1 与 S2 前 n 个字符组组成的字符串完全相同。
输入格式
第一行一个整数 n,表示单词种数。(0<n<100000)
第 2 行到第 n+1 行,第 i+1 行包含一个正整数 w[i],表示第 i 种单词的出现次数m。(1<m<80000)
输出格式
输出一行一个整数,表示整篇文章重编码后的最短长度。
样例输入
4
1
1
2
2
样例输出
12
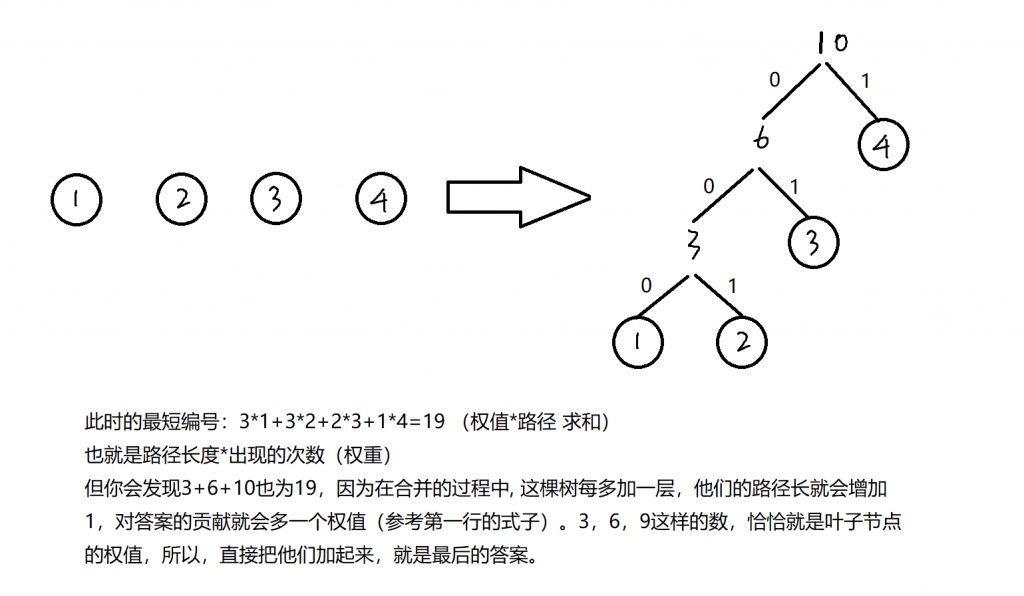
哈夫曼编码各位应该都比较熟悉,最开始森林中都是节点,然后挑选两个权重最小的节点合并成一颗树,这颗新树的权值是两个节点和,然后把这颗树放回去,再挑两个权值最小的树,直到森林中只有一棵树,就结束迭代,主要用到的算法思想是贪心。
代码如下:
#include<iostream>
#include<queue>
using namespace std;
priority_queue<int ,vector <int> , greater<int> > pque; //定义一个维护森林的优先级队列,这样我们的取小操作可以到达O(logn)的级别,关于优先级队列,我也会写一篇博客来描述
int getAnswer()
{
int sum = 0;
while(pque.size() > 1) { //如果森林中只有一棵树就停止迭代
int weight = 0;
for(int i = 0 ; i < 2 ; ++i) { //取两个最小的迭代
weight += pque.top();
pque.pop();
}
sum += weight; //将本次合并对答案的贡献加入答案
pque.push(weight); //再将新的元素加入队列
}
return sum;
}
int main() {
int n;
scanf("%d" , &n);
int tmp;
for(int i = 0 ; i < n ; ++i) {
scanf("%d" , &tmp);
pque.push(tmp); //将元素都存入队列中
}
printf("%d\n" , getAnswer());
return 0;
}
sum+=weight;这条语句用到了哈夫曼树的一个性质,这也是为什么我们不用模拟出一棵树,而直接就可以得到答案的原因。
起泡排序
也就是冒泡排序,我想这么经典的算法应该不用我多赘述了。。。
题目如下:
有 n 名学生,它们的学号分别是 1,2,…,n。这些学生都选修了林老师的算法、数据结构训练营这两门课程。
学期结束了,所有学生的课程总评都已公布,所有总评分数都是 [0,100] 之间的整数。巧合的是,不存在两位同学,他们这两门课的成绩都完全相同。
林老师希望将这些所有的学生按这两门课程的总分进行降序排序,特别地,如果两位同学的总分相同,那林老师希望把算法得分更高的同学排在前面。由于上面提到的巧合,所以,这样排名就可以保证没有并列的同学了。
林老师将这个排序任务交给了他的助教。可是粗心的助教没有理解林老师的要求,将所有学生按学号进行了排序。
林老师希望知道,助教的排序结果中,存在多少逆序对。
如果对于两个学生 (i,j) 而言,i 被排在了 j 前面,并且i 本应被排在 j 的后面,我们就称 (i,j) 是一个逆序对。
请你先帮林老师把所有学生按正确的顺序进行排名,再告诉他助教的错误排名中逆序对的数目。
输入格式
第一行一个整数 n,表示学生的个数。
第 2 行到第 n+1 行,每行 2 个用空格隔开的非负整数,第 i+1 行的两个数依次表示学号为 i 的同学的算法、数据结构训练营的总评成绩。
输出格式
输出包含 n+1 行。
前 n 行表示正确的排序结果,每行 4 个用空格隔开的整数,第 i 行的数依次表示排名为 i 的同学的学号、总分、算法成绩、数据结构训练营成绩。
第 n+1 行一个整数,表示助教的错误排名中逆序对的数目。
样例输入
3
95 85
90 90
100 99
样例输出
3 199 100 99
1 180 95 85
2 180 90 90
2
样例解释
学号为 3 的同学总分为 199,是最高的,所以他应该排第一名。
学号为 1 的同学虽然总分与学号为 2 的同学一致,但是他的算法成绩更高,所以在排名规则下更胜一筹。
原错误排名中的逆序对数目为 2 ,这些逆序对分别为 (1,3) 和 (2,3)。
数据范围
对于 25% 的数据,保证 n=3。
对于 50% 的数据,保证 n≤10。
对于另外 25% 的数据,保证所有同学的总分两两不同。
对于 100% 的数据,保证 n≤5,000 ,且保证不存在成绩完全相同的学生。
时间限制:10 sec
空间限制:256 MB
#include <bits/stdc++.h>
using namespace std;
vector<int> getAnswer(int n, vector<int> A, vector<int> DS) {
vector<int> sum, id; //记录总分和编号
vector<int> ans; //返回值
for(int i = 0 ; i < n ; ++i) {
id.push_back(i + 1); //将编号录入
sum.push_back(DS[i] + A[i]); //将总分录入
}
int cnt = 0; //记录逆序对个数
for(int i = 0 ; i < n ; ++i) {
for(int j = n - 1; j > 0 ; --j) { //除了要判断总成绩之外,题目还要求:当两者成绩相同时,按算法的来
if(sum[j] > sum[j - 1] || sum[j] == sum[j - 1] && A[i] > A[i - 1]) {
swap(id[j], id[j - 1]);
swap(sum[j] , sum[j - 1]);
swap(A[j] , A[j - 1]);
swap(DS[j] , DS[j - 1]);
cnt++;
}
}
}
for(int i = 0 ; i < n ; ++i) {
ans.push_back(id[i]);
ans.push_back(sum[i]);
ans.push_back(A[i]);
ans.push_back(DS[i]);
}
ans.push_back(cnt);
return ans;
}
int main() {
int n;
scanf("%d", &n);
vector<int> A, DS;
for (int i = 0; i < n; ++i) {
int a, ds;
scanf("%d%d", &a, &ds);
A.push_back(a);
DS.push_back(ds);
}
vector<int> ans = getAnswer(n, A, DS);
int cnt = 0;
for (int i = 0; i < n; ++i) {
printf("%d %d %d %d\n", ans[cnt], ans[cnt + 1], ans[cnt + 2], ans[cnt + 3]);
cnt += 4;
}
printf("%d\n", ans[cnt]);
return 0;
}
在冒泡排序的过程中,交换的次数,就是逆序对的个数。







Comments NOTHING