数学建模——拟合

与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好。

一般情况下，当样本数n>30时，表示大样本，可以使用拟合算法；当n<30时，样本量不足，可使用前面提到过的插值算法。

若要对一组数据进行拟合，可以直接使用matlab强大的曲线拟合工具箱。APP——curve fitting，低版本的matlab在命令窗口中输入cftool。

例如如果要对一组变量作拟合：

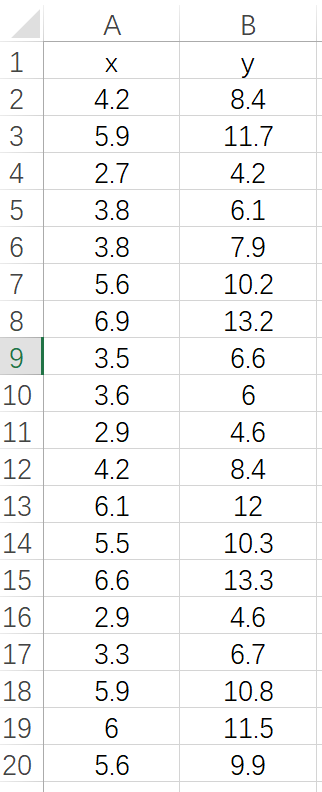
将变量导入到工作区后，打开曲线拟合工具箱：

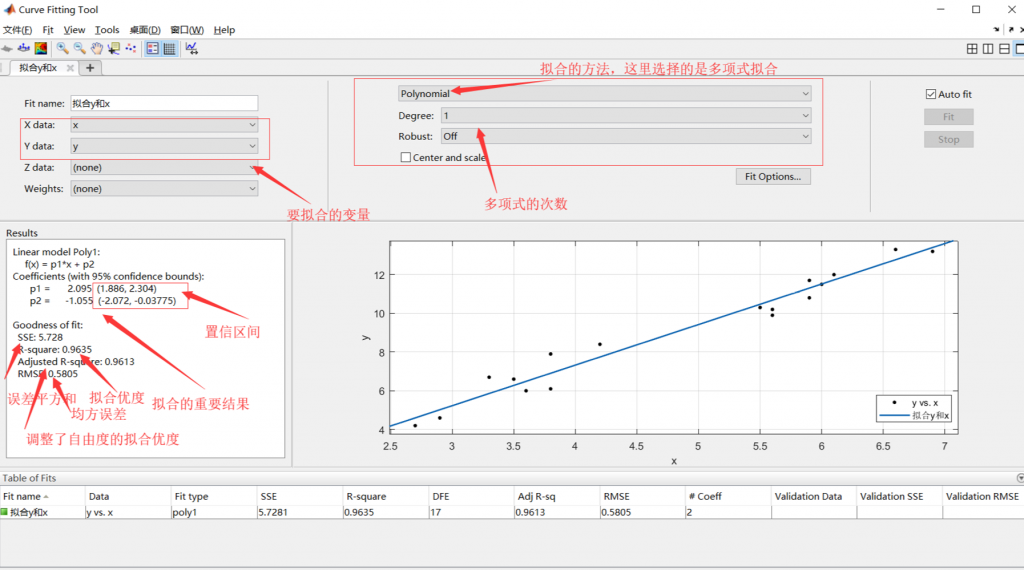
这样，曲线就拟合好了，现在要对拟合的结果做一个评估：

拟合优度：R-sequare（也就是R的平方）
总体平方和：SST
误差平方和：SSE
回归平方和：SSR
可以证明：0 <= R-sequare = SSR/SST = (SST-SSE)/SST = 1 - SSE/SST <= 1

R-sequare越接近于1，说明误差平方和越接近于0，误差越小说明拟合的越好。
注意：R-sequare只能用于拟合函数是线性函数，作为一个评判，如果是其他类型，比如指数，可以直接看SSE。

有时可以自己构造随机数来演示：

% （1）randi : 产生均匀分布的随机整数int  
%产生一个1至10之间的随机矩阵，大小为2x5；
s1 = randi(10,2,5)
%产生一个-5至5之间的随机矩阵，大小为1x10；
s2 = randi([-5,5],1,10)

%  （2） rand: 产生均匀分布的随机数
%产生一个0至1之间的随机矩阵，大小为1x5；
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵，大小为1x5；  % a + (b-a) * rand(1,5); 如：a,b = 2,5
s4= 2 + (5-2) * rand(1,5)

% （3）normrnd:产生正态分布的随机数
%产生一个均值为0，标准差为2的正态分布的随机矩阵，大小为3x4；
s5 = normrnd(0,2,3,4)

% （4）roundn—任意位置四舍五入
% 0个位 1十位  2百位 -1小数点后一位  
a = 3.1415
roundn(a,-2)    % ans   =  3.1400
roundn(a,2)      % ans   =  0
a =31415
roundn(a,2)   % ans  = 31400
roundn(5.5,0)  %6
roundn(5.5,1) %10