这套试卷是今天上午做的,三个小时拉满了,不过做的倒是还挺好的,选填一共错了一个,第二个大题的计算结果没有化简,数列极限证明那个极限为零写的不清楚,然后二重积分的计算有个地方抄掉了个cos,其他地方就没什么问题了,感觉整体的难度比前两套都要稍微小一些,当然也有可能只是这套卷子更加符合我的胃口,和我做过的题挺契合。
下面开始复盘

第一条道题不难的,直接除$x$然后用泰勒算就行了

第二题也不难,我们来逐个分析
首先A选项,瑕点为$x = 1$,此时分母可以写成$(x - 1)(x + 1)\sqrt{1 + x}$,此时$x - 1$那一项就只有一次,那么根据$p$积分可以知道肯定就发散了
再看B选项,考虑$x \to \infty$的情况,此时可以对式子进行放缩:$\frac{1}{(x + 1) ^ 2 \sqrt[]{1+x} } < \frac{1}{x^{\frac{5}{2}}}$,后面那个根据$p$积分可以知道是收敛的,因此就能推前面收敛了,所以b选项是正确的,其他的选项也用类似的方法推就行了。

这道题和第二套的那个填空题如出一辙,而且前面那套更难一些,需要两次泰勒,这道题用一次泰勒以后,第二次的那个拉格朗日想法挺自然的,难度不大。

这道题也不难,首先把面积和对角线的长度用$xyz$表示出来,它们都是关于$t$的函数,然后对表达式进行$t$的求导就好了。

几乎没有难度,只需要知道怎么先$\theta$后$r$就能出来了,主要就是要知道$rdr$是一个整体的,然后就能立马选出来了。

难度也不大,就按照题目的意思求偏导,需要稍微细心一些。

根据所给的解的形式,可以先把方程给推出来,然后再根据方程就能把微分方程的解给求出来了,带入求极限就行,当然还有一种题,你不需要把微分方程的解求出来,只需要把y表示出来然后带入式子求极限就好了,880上第一章的综合体就有类似的题。

这道题也很简单,拼起来做行变换然后考察是否可以线性表示就行了
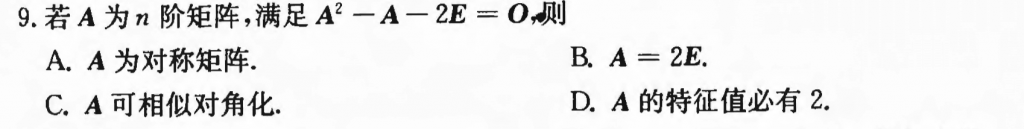
根据秩来推,首先可以知道$(A+E)(A-2E) = 0$,然后就有:$R(A + E) + R(A - 2E) \le n$,再根据$R(A + E) + R(A - 2E) = R(A + E) + R(2E - A) \ge R(A + E + 2E - A) = n$,然后便可以知道有$n$个线性无关的特征向量,那么就可以相似对角化了。
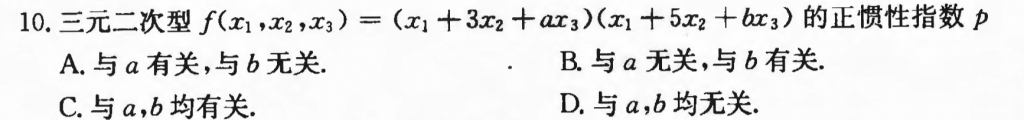
这道题我是蒙对的,做的时候确实没有想到要两次换元,我先暴力把这个括号打开,然后把二次型的矩阵写了出来,再想求特征值啥的,发现好像题难求的,然后就转向证明是否是正定或者负定,求了顺序主子式发现二阶顺序主子式是小于零的,而三阶顺序主子式(行列式)等于零,就知道大概寄了,蒙了个D,感觉还是挺好蒙的hh。
正统的方法是先换一次元,变成:$f = y_1y_2$,然后因为这个里头没有平方项,只有交叉项,就考虑作平方差换元,这个应该每个讲义里头都会有,然后就能把惯性指数弄出来了。

也是有些基础的题,此类动态函数先给它分区间化简,然后在分段点处进行判断是否为间断点就好了。

可以知道$f'(0) = 2, f''(0) = 2$,然后要求反函数的二阶导数直接用公式就好了:$-\frac{y''(0)}{y'^3(0)}$,这个公式肯定是要牢记于心的。
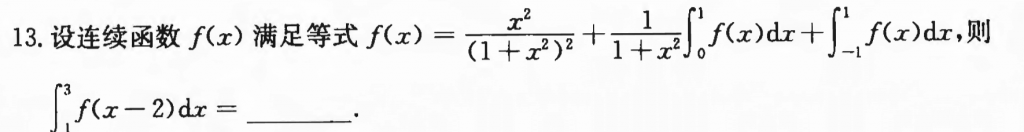
这道题也不难,首先设$\int_{0}^{1} f(x) dx = A, \int_{-1}^{1} f(x) dx = B$,然后带进去,两边算极限,然后可以发现是偶函数,那么$2A = B$,把其中一个求出来即可,然后对于要求的式子,换个元就好了。

唯一错的一道选填题就是这道,看花眼了,还以为两个上限都是1,没想到后一个的上限是$x$,太坑了。。这道题也不难,把xy对调,然后两个积分是相等的,就可以拓展三角形区域为正方形区域,然后再凑微分啥的,就好做了。

这道题如果没见过或者没做过的话估计会挺懵的,但是一般习题册里头应该也会有这样的题,我做往年的超越卷也遇到过,主要是要先对其中一个求导,然后再对另一个求导,最后把y设置为1,这样就可以把关于$f(x)$的微分方程给整出来,再求解微分方程,带入初值就可以把$f(x)$确定下来了。
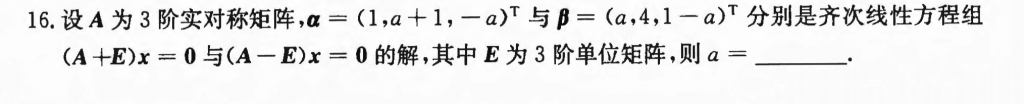
可以知道,$\alpha, \beta$是A的不同特征值所对应的特征向量,那么它们肯定是正交的(实对称矩阵),然后根据内积为零,就可以把a给求出来了。

也是基础题,首先把切线方程写出来,然后把$t$给带进去,然后在求关于$x$的极限的时候,利用换元把$x$换成$t$,然后求极限就好了。

难度不大,主要是第二问算的恼火,首先求那个x的坐标就挺麻烦的,我换了个元$e^x = t$,然后再用求根公式啥的,然后把$x$给整出来,然后再算$y^2$,以及定积分的计算也都挺恼火的,需要沉下心来计算。
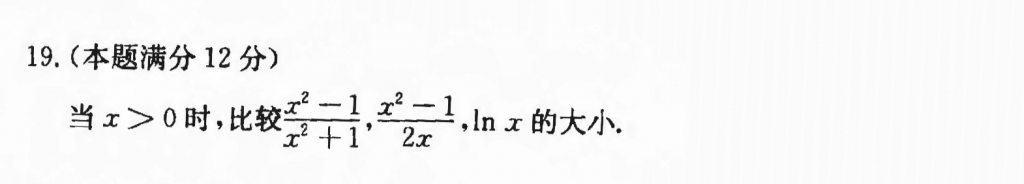
感觉这种题试探性挺强的,我首先考虑的是前两个,因为它们的分子是相同的,根据正负然后比较分母的大小就好了,然后当把$lnx$加入比较的时候发现走了弯路,$lnx$是个中介,让它和前两个分别比较就可以把大小关系弄出来,构造辅助函数,用单调性就行了。

第一问的单调有界应该没太大问题,有界就用归纳法,单调性就用后项减前项,然后可以证明出极限存在。主要是要证明这个极限等于零我感觉挺麻烦的。我没裹清除,扣了几分,答案是推出$A \ge 0$,然后否定掉$A \gt 0$的情况,然后就等于零了。
第二问也挺简单的,根据第一问实际上可以知道$f(0) = 0$,可以直接用泰勒,然后带进去,或者洛必达一次,然后分子可以凑拉格朗日,然后就可以把极限给整出来了。

这道题刚看到可能还有些懵逼,但是其实可以划分两个区间,这两个区间是泾渭分明的,然后再用极坐标就可以了,计算量也很小,但是要细心!!!我不知道怎么就抄掉了个cos。。


这题纯粹是来凑数的,基本都是习题册或者讲义里头的原题,首先第一问的$\beta$可以用A的特征向量来线性表示,然后就可以用特征值特征向量的定义了。
第二问也简单,属于是相似的基本应用题。
复盘结束,码字较快,如果有什么问题欢在评论区与我交流,感谢阅读。







Comments NOTHING