这套卷子是今天上午做的,终于一次是按照规定来了,正常的模拟数学的时间,做了这套卷子。
客观评价这套卷子的难度,我感觉难度不大,但是也做了三个小时,倒不是说计算量有多大,主要是在计算的过程中频频出现失误。。要经常回头DEBUG,导致拉低了做题时间,粗心的问题比较难改。
下面开始复盘:

第一题的难度不大,$\{an\}$无界,那么就可以自定义一个比较特殊的数列,这个数列里面有一个点是无穷,其他的点都是一样的,那么A的说法就是正确的,趋于无穷的子列就是那个无穷的点,收敛的子列就是其他的点组成的子列。
BCD选项,每个子列都收敛或者无穷或者无界(?)

这道题目也不难,可以用奇偶性,然后变形比较就好了。

偏导存在啥也推不出来
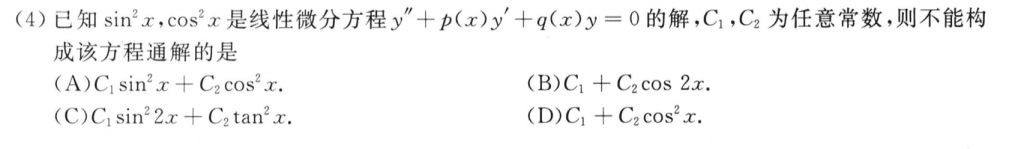
这题有意思,答案的思路很清晰,既然$sin^2x, cos^2x$是线性微分方程的解,那么$C_1sin^2x + C_2cos^2x$可以构成通解,B和D都可以变形成这个通解的形式。
我当时做的时候没想到这个,我把这俩解直接带到了这个方程里头,然后可以推出来$q(x)=0$,然后就把BD带进去,发现是可以满足方程的,然后就选c了。

这题我感觉也挺难了,还想了好久,主要是看到了D选项,然后就想起来了估计是要用奇偶,换个元发现还真是,然后就选了D。

这题简单的,就是原函数存在定理,如果是连续,那么一定存在原函数,如果有第一类间断点,那么一定没有原函数,可以很快验证C是有跳跃间断点的,所以不存在原函数了。
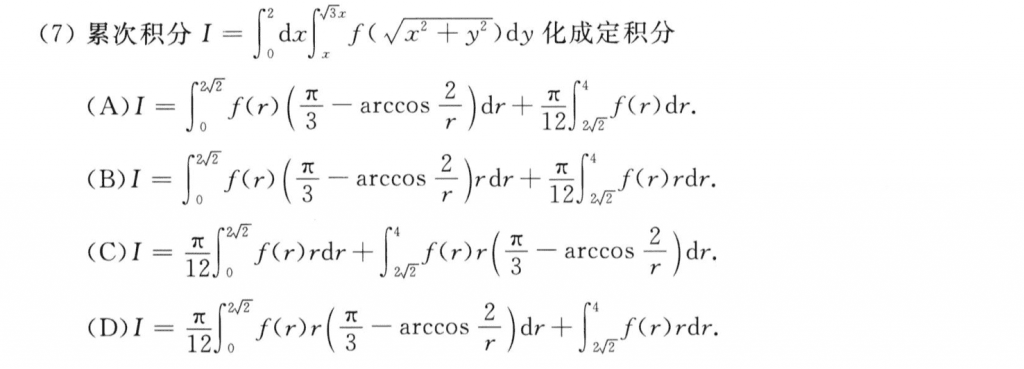
这题就先$r$后$\theta$,然后就出来了,不难。

用分块矩阵的乘法,基础题
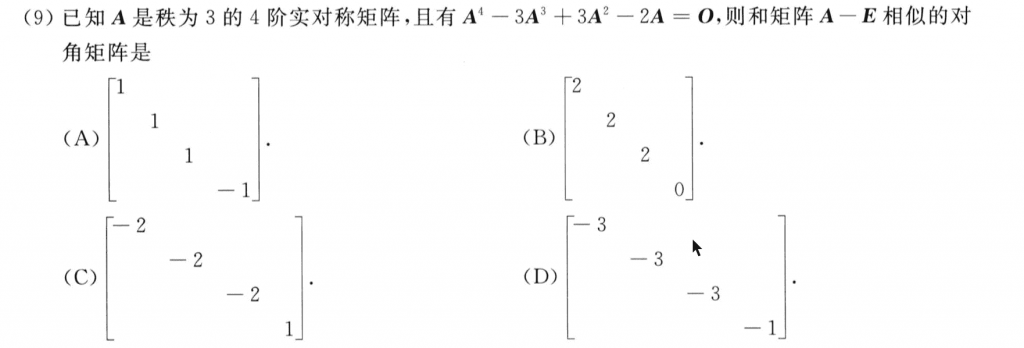
可以先根据所给的矩阵方程得到A的特征值的集合,然后根据秩是3就可以把特征值确定下来。

考试的时候直接蒙了一个,复盘的时候也没有想出什么比较好的方法,比较难,还是根据答案的思路来,虽然有点看得云里雾里的。

细节题,要分两种情况,交点有两个,一个是$x = 0$,另一个是$x = 1 - $k,根据$k$的不同,那么在进行计算的时候谁在下面,谁在上面也是不知道的,所以需要分情况讨论。
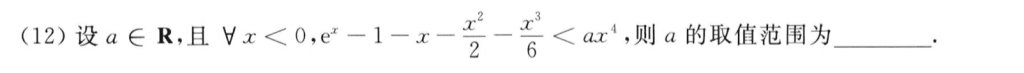
泰勒展开放缩,不过这道题好像挺有争议的,据说端点也可以取。
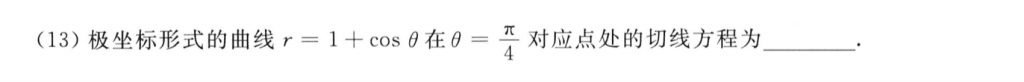
基础题

基础题,主要是平均值的公式记得就行,然后就硬算就完了,

直接pass,啥玩意角速度,死去的回忆突然攻击人?

这题不难,直接把$A_1$用$A$表示,然后$B_1$用$B$表示,然后带进去就行。
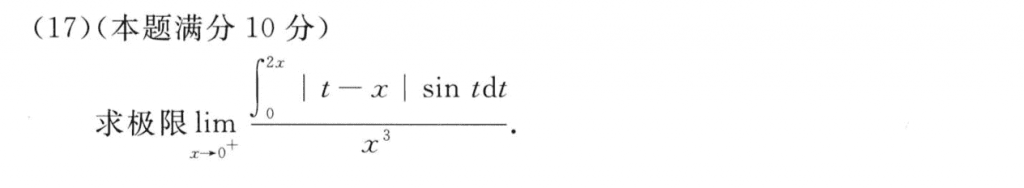
先换元,然后sin的那一项用公式变成$sincos+cossin$的形式,再用洛必达什么的随便搞就行了

这题计算还是比较麻烦的,不过这种过一点作曲线的切线的题已经做了很多个了,这题就求导稍微麻烦点,不过也有小技巧,比如把根号里头的东西打开,然后配方,再求的话感觉会稍微简单一些。
第二问主要是要分区间,不要像我一样直接从$\frac{5}{2}$到4积分。。

不难,很常规的构造辅助函数,没有难度

这题第一问难的
第二问不难,就换元
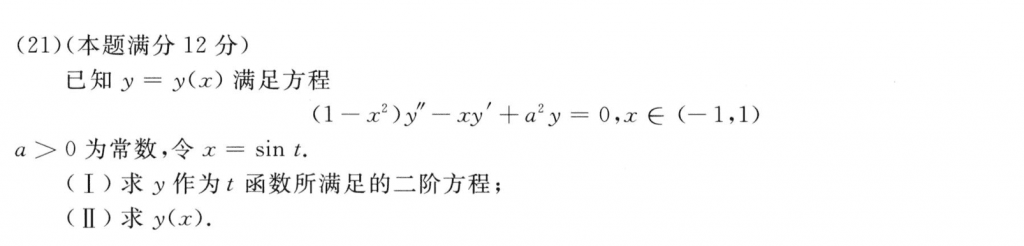
这题感觉好像在超越还是在哪也做过,也不难。

主要是$A\alpha = 3\beta, A\beta = 3\alpha$这俩条件的使用,把这俩式子相加和相减可以得到关于特征值和特征向量的条件,然后三个特征值和三个特征向量,第二问就用初等变化来求A。
第三问用配方法就用配方法,还好第二套出了个配方法,赶紧速成了一波,做这道题就不难了hh。
复盘over,码字较快,可能会有一些小问题,欢迎在评论区与我交流,感谢阅读。







Comments NOTHING