这张试卷是今天晚上做的,一个多小时就写完了,结果错了三个选择题,有个填空题多搞了个负号...以后做卷子还是得稍微细心一些。
客观评价这套试卷,我感觉选择题的质量很高,对概念的考察很细,可以做到查漏补缺的效果,填空题马马虎虎,计算量不大,大题拉胯,除了那道概念性质的证明题有点稍微开眼界以外,其他基本都是很常规的题,甚至第一题直接就是某一年的真题,我这两天才刚刚做过。。
下面开始复盘:

第一题既然要求值域,那么也就是要求最大值和最小值,对函数求导发现是单调递增的,最小值就是在负无穷,最大值是在正无穷。

第二题我做错了,果然对结论的使用还是不太熟练,现在一个一个来分析
- 首先A的话可以直接用结论,也就是等于上限的阶数乘被积函数加一的阶数
- B的话对于被积函数可以直接用等价无穷小:$1-(cosx)^l\sim \frac{l}{2}x^2$,然后积分限要取低阶的
- C的话,积分限是同阶非等价,所以也可以直接用结论
- D不能直接用结论啊,我就是直接用结论搞错了,这种等价的需要具体问题具体分析,答案用的是积分中值定理,学到一手!

第三题也是好题
- 选项A,对于$x_0$处可导的函数确实是这样,那对于不可导的就不好说了
- 选项B,二阶三阶导可能都为零,然后四阶导大于零
- 选项C,没说是连续函数
- 选项D是正确的
答案有个总结非常好:

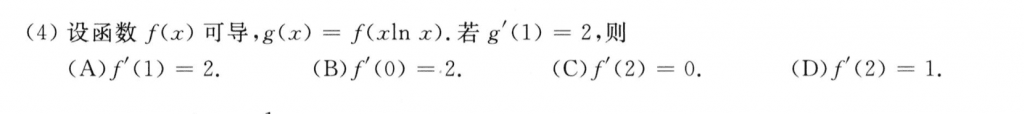
这题简单

这题简单

第六题我做错了。。
其实不难,AB应该挺好判断正误的,主要是C和D,对于D的话,可以知道其实在$x$轴方向的变化是要比$y$轴方向快的,那么x轴增加一个单位肯定比y轴增加一个单位要大,所以应该是小于号。
用答案那个构造辅助函数的方法也挺好的,不过想不到。。
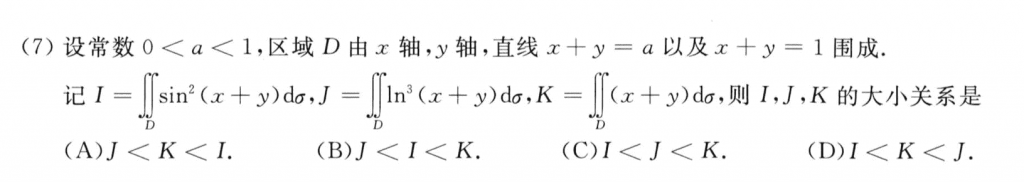
第七题,ln那个肯定小于零了,然后$sin^2x < sinx <x$

第八题也不难,秩一矩阵的特征值是非常重要的,它的一个特征值是两个向量的内积,其余特征值都是零,然后矩阵A最小特征值对应的特征向量和$\beta\alpha^T$所对应的特征值的特征向量是同一个。

首先可以知道$\alpha_1, \alpha_2$是线性无关的,然后$\beta_1, \beta_2$也是线性无关的,而$\beta, \alpha$的内积是零,也就是说他们是垂直的,所以肯定都是线性无关的。
不知道我上面的这个逻辑有没有问题,答案的过程比较严谨

这题我做错了,好题,二次型对应的标准型是不唯一的,只有正负惯性指数是一定的,所以求出来$A+kE$的三个特征值以后,他们都大于零,就可以把k的取值范围给推出来。

这题不难

这题也不难,分子拉格朗日一下
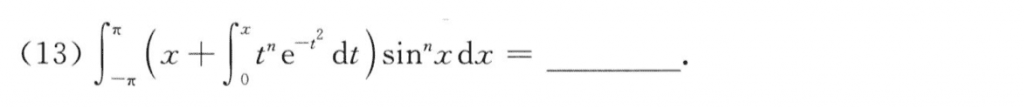
这题一看就是要先分析奇偶性,而被积函数的奇偶性是和$n$相关的,所以需要分$n$是奇数还是偶数。

这题我多了个负号。。。就常规的部分分式分解就好了

送分题,换个元,然后求导啥的就好了

$A^TA$正定,可以推出$A$的特征值里面没有零特征值,所以行列式不为零,然后就可以把a求出来了

这题就是某年的真题,改都没改

套公式,基础中的基础
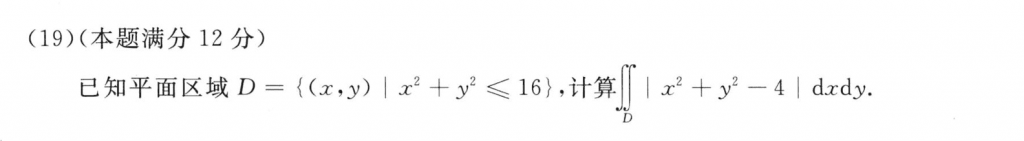
分块去绝对值,也是基础题
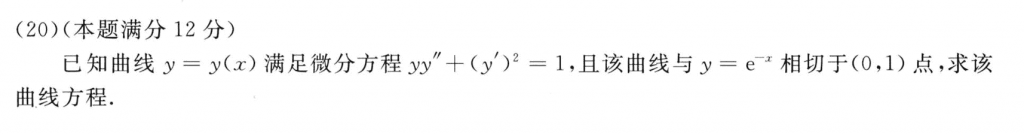
这题感觉我应该会被扣一些过程分,实际上也不难,首先可以知道肯定要降阶,而且是不含x的降阶模式,然后就可以分离变量了。
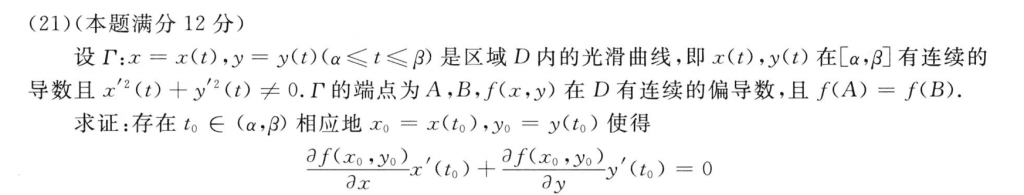
实际上非常简单的一道题,不要想复杂了,首先罗尔定理肯定是可以想到的,所以要设一个关于$t$的一元函数,然后利用条件,用罗尔定理就一步到位了
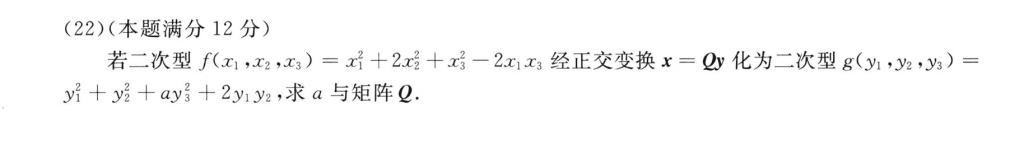
这题也不难,主要是用对角矩阵作为一个过渡矩阵,来推出Q,这题答案不唯一,相信自己!







Comments NOTHING