这张试卷是今天上午做的,因为稍微难一点的题目基本都做过,所以做起来也没有什么压力,比较新颖的就是那道数列极限结合方程的压轴题,如果在考场上第一次见到估计会挺懵的。

第一题不难,因为正无穷和负无穷都有水平渐近线,所以就不用浪费时间考察斜渐近线了
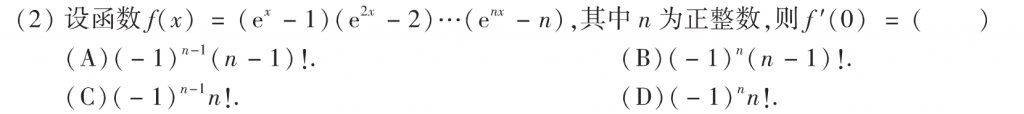
这题也是比较经典的题,用导数定义挺方便的
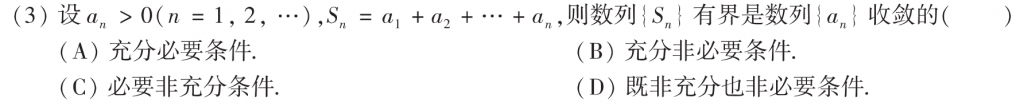
这题难的,整张卷子最难的题了,首先要知道$a_n = S_n - S_{n-1}$,然后$a_n > 0$可以知道$S_n$是单调递增的,如果$S_n$有界,那么单调有界,$S_n$肯定就收敛了,进而可以推出$a_n$收敛。
对于$a_n$收敛,可以设$a_n = 1$,这个时候$S_n$依旧是发散的

这道题最快的方法就是武老师讲的画图的方法来判断,先把$sin$的图像画出来,然后因为$e^{x^2}$是单调递增的,所以$sin$是越来越大的,然后分成三块判断就好了,其他的方法就做差比较。
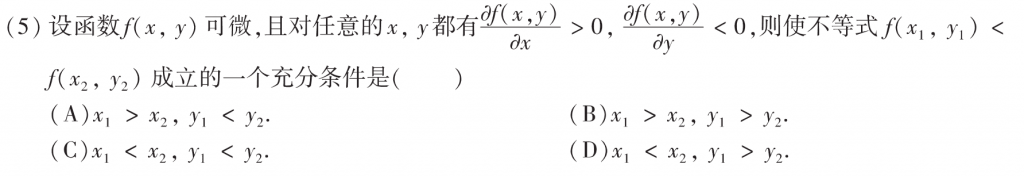
这题不难,在$x$轴方向上单调递增,在$y$轴的方向上单调递减,然后就知道$x_1, x_2, y_1, y_2$之间的大小关系了
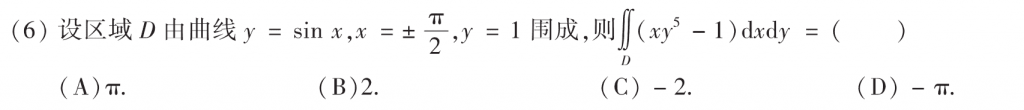
经典题,主要是做辅助线,然后分区间用奇偶性
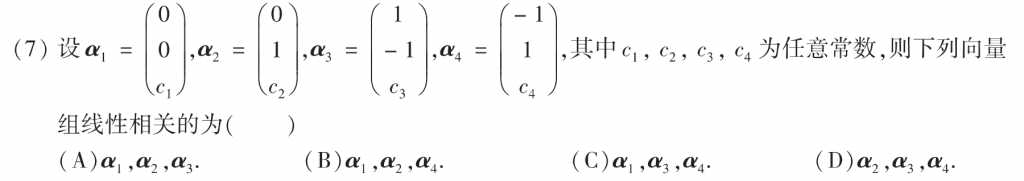
考察行列式,$\alpha_1, \alpha_3, \alpha_4$的第二行可以变成零,那么就说明他们是相关的了

把Q写成P乘一个矩阵,然后带进去就好了
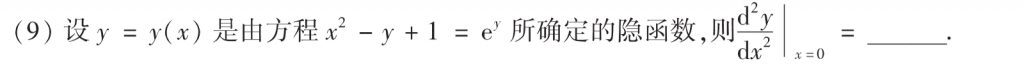
基础题,pass
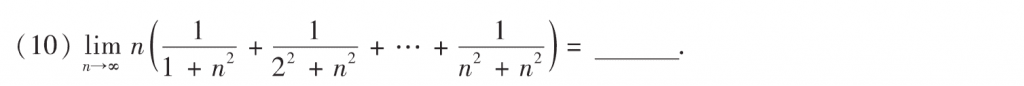
定积分定义,提分母的$n^2$出来,然后和前面的$n$抵消一个,就变成可爱因子了

基础题

把$x$看成函数,$y$看成自变量
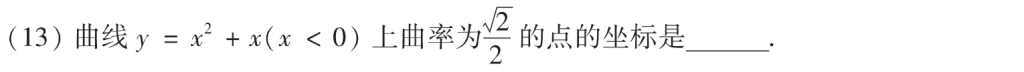
套曲率的公式就好了,基础题

行列式交换两行是要多一个负号的,这个细节别忘了

这题也不难,直接计算极限就好了

基本题,求ABC判断$AC-B^2$

这题我被坑了。。题目没看清楚,还以为那个B点是切线和x轴的焦点。。。离谱,本来套公式的题。
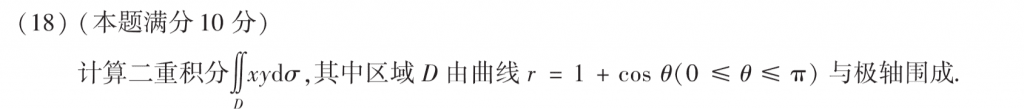
这题我是暴力算的,主要是那个$(1 + cos\theta)^4$,要耐心算出来,也可以用换元的方法,这样算下来是最快的,不过真正做题的时候我确实没有想到。
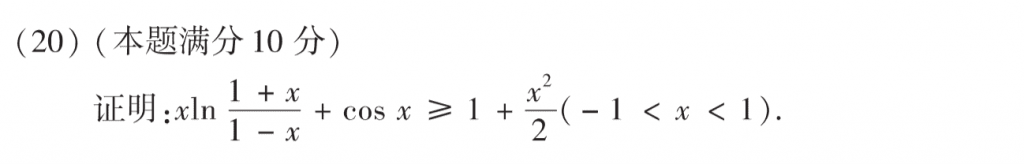
首先意识构造的函数是一个偶函数,就可以把要证明的区间缩小一半的,感觉真题里面很多题都会用到这个,比如2010年的解答题里面就出现过类似的思想。
然后求完一阶导数以后,是一个稍微有些麻烦的式子,对这个式子是可以直接进行放缩然后判断符号的。

这题感觉是比较新颖的一道题,首先有且仅有一个实根,并且没有涉及到导数,那么肯定往零点定理的方向考虑,主要是要用一下等比数列的求和公式。
第二问单调有界,其中有界性在第一问实际上就已经知道了,那么对于单调性,就用$x_{n+1} - x_n$,然后判断符号就好了。这样就可以证明数列收敛,然后就可以直接计算数列的极限了。
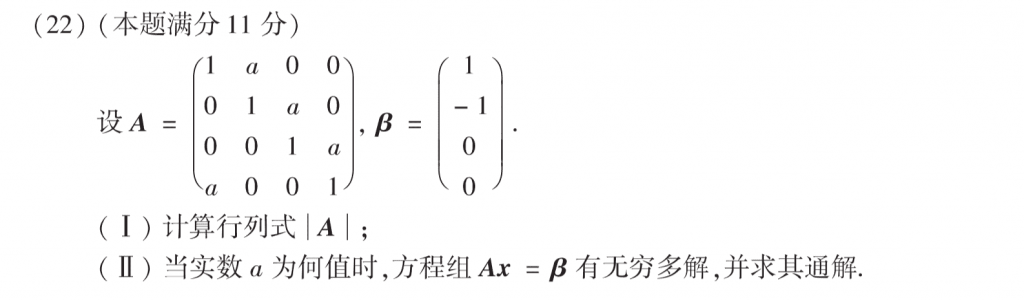
算det(A)直接找一行或者一列展开就行了,不用整那么多有的没的。
然后第二问就用一下第一问求出来的行列式,既然有无穷解,那么行列式肯定是为零的,只不过需要排除无解的情况。

$R(A^TA) = R(A)$,这是一个常用结论,然后就可以对A直接进行操作了,然后把a给求出来。
第二问也挺常规。







Comments NOTHING