这张卷子是今天上午做的,三个小时做满了,感觉绝对难度比前两套都要更难一些,计算量也挺大的,但是难而不偏,质量很高。
现在开始复盘

第一题我就做错了,这种概念题放到第一题挺麻烦的,要一个一个分析
补充一个知识点:
- 如果$f(x)$是奇函数,那么$\int_{a}^{x} f(x)dx$就是偶函数(全体原函数都是偶函数)
- 如果$f(x)$是偶函数,那么$\int_{0}^{x} f(x)dx$就是奇函数(只有下限为零的才是奇函数,因为要保证$f(0) = 0$)
首先A的话可以举一个例子,比如$f(t)$的原函数是$F(t)$,就可以选一个$F(a) = 0$的函数,比如$sin(2\pi)$。
B应该是很好排除的,一个周期函数的原函数为周期函数,还需要一个条件:在一个周期上的积分为零
C是正确答案,首先$f'(x)$是奇函数,那么$f(x)$一定是偶函数,以0为下限的变限积分就是奇函数了,符合前面补充的知识点
D是不正确的,$f'(x)$是偶函数,那么$f(x)$不一定是奇函数,需要保证$f(0) = 0$
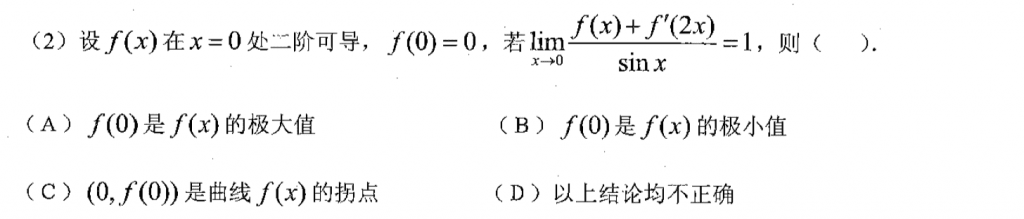
第二题不难,我用的是保号性做的,可以推$f'(x)$在$x=0$两侧的正负情况

第三题其实还是非常难的,但是选项设置的太拉了,很显然可以知道答案在C和D里面选,那么A和B就一定是对的,如果B是对的,那么C就一定是错的。。这个逻辑应该没问题。
正常来做的话,首先用奇偶性可以推AB正确,比如$f(x)$很显然是偶函数,那么2015次导就是奇函数,然后AB就可以证明是正确的了。
对于CD的话,就需要分析在$x=1, x= -1$处的高阶导数,答案用的是莱布尼茨公式,实际上也可以用泰勒,而且用泰勒会更加简单:$f(x) = (x^2 - 1)^{2015} = (x-1)^{2015}(x+1)^{2015}$,当需要分析$x=1$的高阶导数时,就考虑保留$(x-1)^{2015}$的那一项(考虑一下为什么?),然后对$(x+1)^{2015}$进行泰勒展开,实际上因为题目要求2015阶导数,而前面$(x-1)$已经提供了2015次方,所以后面的那个$(x+1)^{2015}$只需要变形:$[(x-1) + 2]^{2015}$,然后取常数项:也就是$2^{2015}$,这个就是泰勒的那个系数了,然后再乘上2015的阶乘,就得到$f^{(2015)}(1)$的值了,同理$x=-1$也是如此,看着复杂,实际非常简单。

第四题不难,根据特解的形式可以推出特征方程的特征根,然后再倒推微分方程就好了。
$e^xsinx$可以知道特征根为$1 \pm i$,然后$x$可以知道肯定是$(c_1x+c_2)e^{0x}$的形式,所以0是二重根,然后就ok了。

这道题我直接就从D开始入手,然后就整出来了,因为$sin^nt$肯定是周期函数,如果它在一个周期上的积分为零,那么就可以知道$f(x)$也是周期函数了,证明方法也很常规,就换元然后用奇偶性。

需要放缩,比较被积函数的大小就好了。

把$A\alpha$写成特征值的形式,然后再用分块矩阵的乘法可以把这个向量组写成三个$\alpha$和一个矩阵相乘的形式,然后只需要后面那个矩阵的行列式得零就可以知道他们相关了。

$A^2$正定,只能知道$A, A^*$的特征值的平方都是大于零的,不能推出$A, A^*$的特征值大于零,只能说他们的特征值里面没有零特征值,也就是可逆。

我直接设$f(x) = x^3 - \lambda x + 2$,然后分析函数形态:
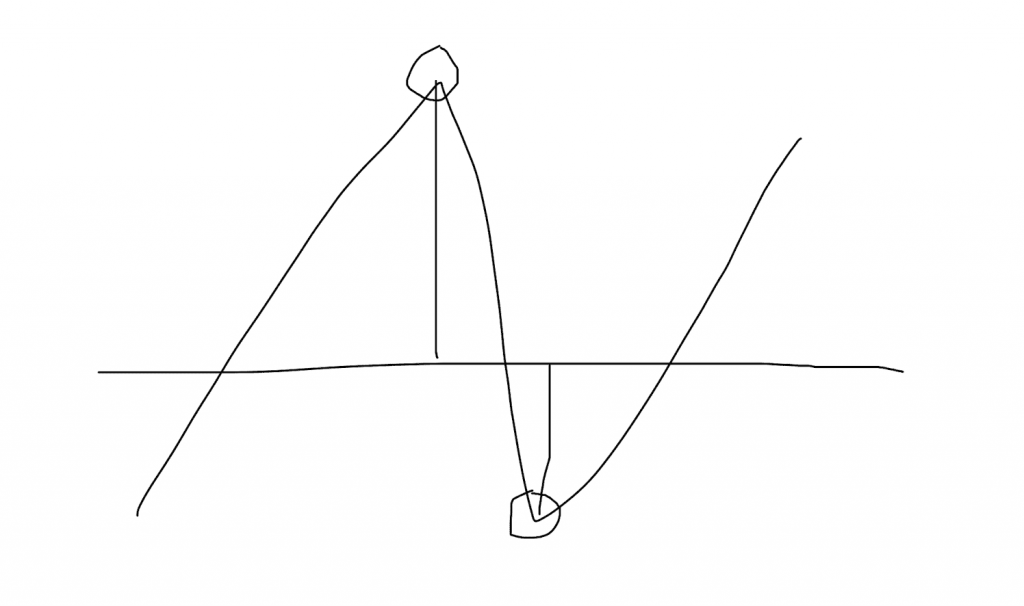
当这两个画圈的点分别大于零和小于零的时候就有三个不相等的实根了,稍微有些麻烦
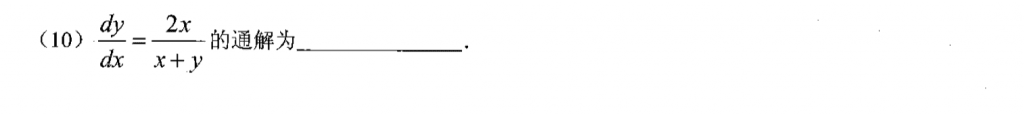
齐次微分方程,不太难

其实就是圆绕着$y$轴旋转,然后要求旋转体的体积,直接用公式套就行了。

基础
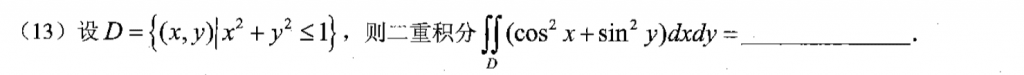
积分区域关于$y=x$对称,就可以用一下轮换对称,然后就可以把被积函数给搞掉了
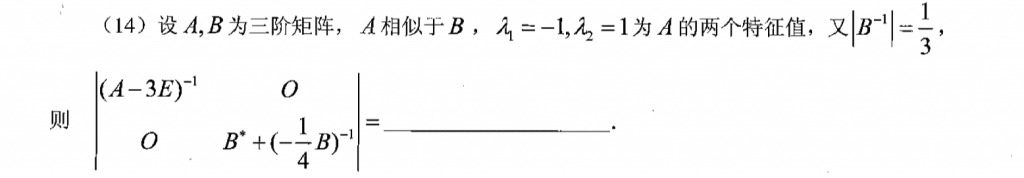
这题算错了,草稿纸上第一行写的就是$|B| = \frac{1}{3}$,算了半天,算了个离谱的答案。。算这种题还是需要保持头脑清醒。

第一问就单调性,第二问的左边部分也是单调性,然后右边部分要用第一问的条件,可以知道$f(x) < f(1), 0<x<1$,然后就可以把右边的推出来。
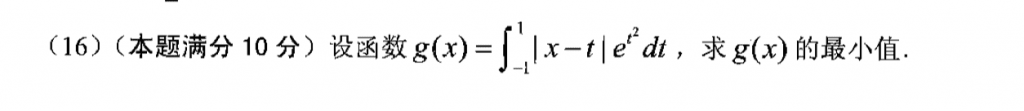
有序没有给x的范围,所以需要分成三段,然后对于每一段分开求极小值。
最后还需要用放缩来判断这三个极小值的大小来确定最小值。
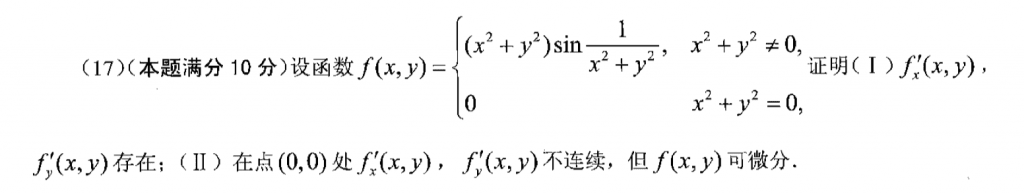
这题也不难,按理来讲这种题应该作为选择题来考的
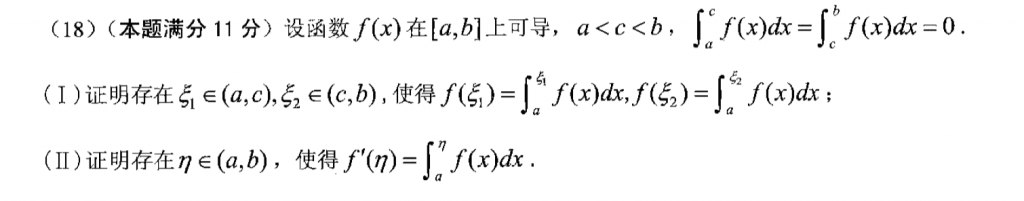
很显然是构造辅助函数罗尔定理的题,在构造辅助函数的时候,这个积分实际是有些碍眼的,可以令$F(x) = \int_{a}^{x}f(t)dt$,然后$f(x) = F'(x)$,这样的话按照最常规的构造辅助函数的方法就好了。
第二问在构造辅助函数的时候发现差了一阶,所以就可以补充个一阶导,来保持平衡,然后辅助函数就构造出来了。
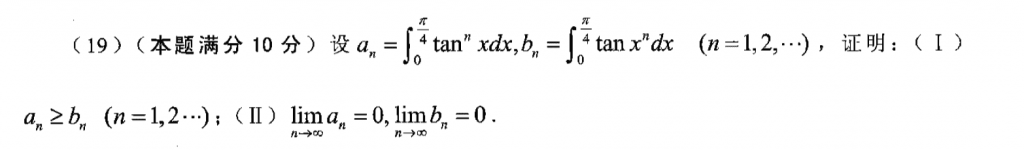
这题我没整出来。。实际也不难,第一问就分析被积函数的大小就好了,做差然后用单调性分析就好。第二问的技巧性挺强的,这种题在考场看到估计直接白给了。

这题严选题上有,而且严选题没有给第二问的那个变量代换暗示,难度就又高了一阶。这题的精华手法就在于用$f(x)$来代替$f'(x)$的一部分。
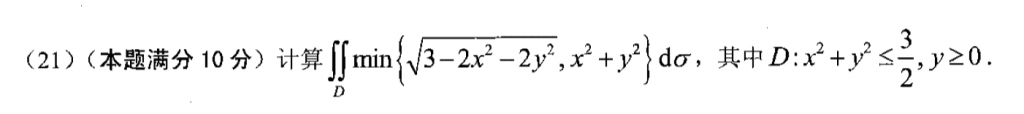
这种题可以先用$t = x^2 + y^2$来划分区域确定被积函数,然后之后就简单了。
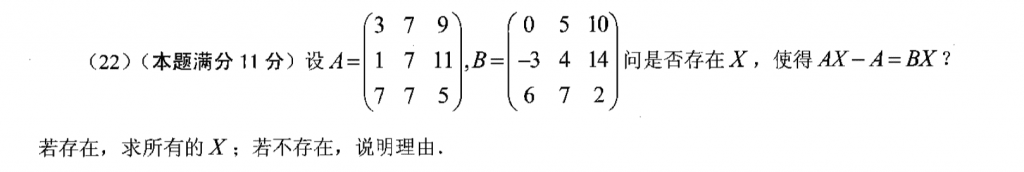
这题也不难,直接$(A-B)X = A$,然后用初等变换的方法,就可以把X给整出来
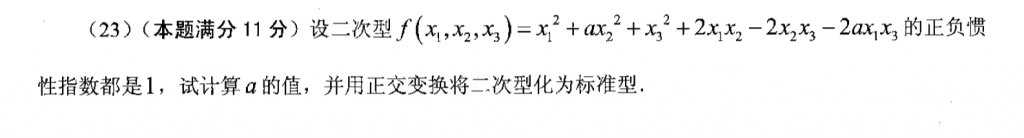
也是基础题,这两天做的真题也有这种考法,把带参数的特征值求出来之后,进行排序,然后中间那个设置为零,就可以把a的值求出来了,然后根据特征值求特征向量,再单位化,拼成Q矩阵,就ok了。
复盘结束,码字较快,可能有一些问题,欢迎评论区交流,感谢阅读!







Comments NOTHING