这张试卷是今天晚上做的,我感觉小题比较拉胯,大题计算量挺大的,题目难度也比零几年的上升了一个台阶。
现在开始复盘
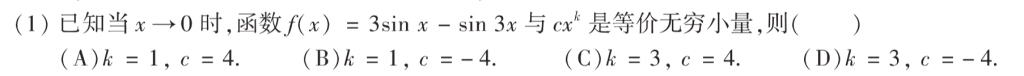
基础题,但是这么显眼的$cx^k$真的好吗?

基础,拆开,然后两次导数定义就好了
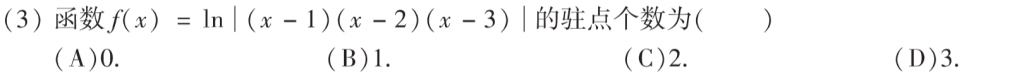
要求驻点那肯定就要先求导了:
$$
f'(x) = \frac{[(x-1)(x-2)(x-3)]'}{(x-1)(x-2)(x-3)}
$$
然后分子部分,$x=1, x=2, x=3$的时候,根据罗尔定理可以知道至少有两个零点,然后又因为是二次多项式,最多两个零点,这样驻点个数就出来了。

第四题也是基础题,后两项那个要用解的叠加性质,分开设解,不能混在一起

$AC-B^2>0, A>0$,就可以得到条件了
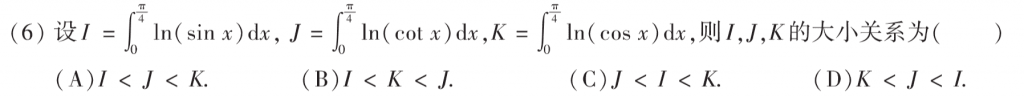
$ln$单调,所以比较积分的大小就可以转化为比较函数的大小:$sinx < cosx < cotx$,然后就出来了

这题我给记混了。。还以为右乘是列变换,导致做错,实际上是非常基础的一道题,着实不应该,要好好反思!

首先A的基础解系里头只有一个向量,那么就说明A的秩为3,然后$A^*$的秩就是1了,基础解系里头应该是三个向量,然后再根据Ax=0的解,可以知道$\alpha_1, \alpha_3$是线性相关的,所以他们肯定不能作为基础解系,然后D就选出来了

$e^\infty$,用三部曲简单
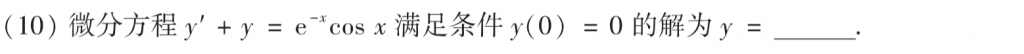
一阶常系数非齐次微分方程,直接套公式就好了

经典题了,套公式就行
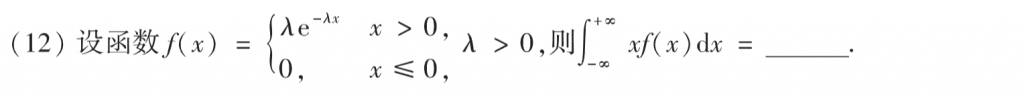
这题也不难,首先格局被积函数可以把区间缩小一半,然后把$f(x)$带进去,就可以把这个积分算出来
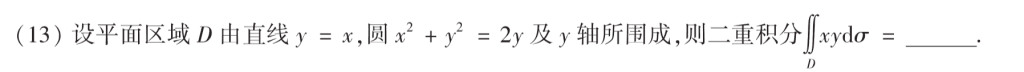
用极坐标
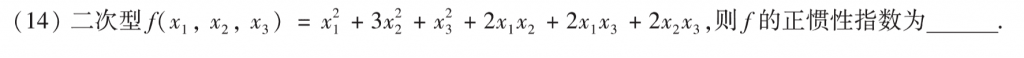
我是求出了三个特征值,用配方法会更快一些,但是我不大会
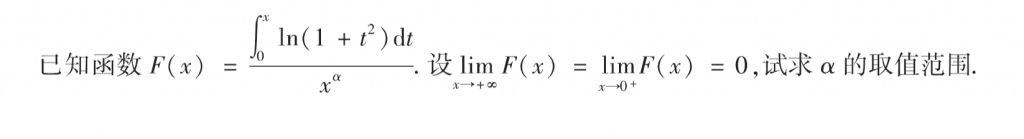
这题也不难,洛必达就可以了

也是基础题,计算也不大难

这题注意用先代后求的手法,求出来$\frac{\partial z}{\partial x}$之后就可以把$x = 1$带进去,化简一步,然后再对y求导

这题需要一点几何基础,实际上$y' = tan\alpha$, 然后就可以把$\alpha$解出来,然后再求导什么的计算微分方程就好了。

第一问直接拉格朗日。
第二问的话先用$a_{n+1} - a_n$把单调性搞出来,然后再用第一问的条件,可以证明$a_n > 0$,单调有界,就可以证明数列收敛了。

又是非常经典的题,这种比较简单的体积问题,直接用公式就好了,不用整什么二重积分,当然也是可以的,但是没必要整那么麻烦。
第二问就计算,吐槽下计算量!

好题,用分部积分一步一步来就可以整出来,武忠祥的辅导讲义上有这道例题,所以就不难了,如果第一次拿到估计有点受不了,得缓缓。

根据秩:$R(\beta_1, \beta_2, \beta_3) < R(\alpha_1, \alpha_2, \alpha_3) = 3$,就可以把a求出来,然后算第二问的时候,直接把把所有的向量都拼在一起,然后整体变换,不用一个一个向量求,没有必要,这样会更快一些。

根据所给的矩阵方程就可以得到两个特征值和两个特征向量,再根据相似对角化和A的秩,可以知道有另一个特征值零,不同特征值对应的特征向量垂直正交可以把第三个向量求出来。
三个特征向量三个特征值,齐活了,直接用初等变换会稍微简单一些。







Comments NOTHING