这张试卷是今天上午做的,昨天因为状态不太行所以没有写模拟卷,做李正元的超越135去了,所以今天做了两套试卷,一张是超越的这张,还有一张是11年的真题。客观来说超越的这张试卷质量依旧很高,解答题我两道题无从下手,物理应用白给,然后中值定理的证命题想了很久也没有想出来。
下面开始复盘。

第一题的1和2很好排除,函数值的大小与导数值的大小并没有什么必然的联系,反例也很好举,3就是定积分不等式的结论了,对于4可以想象$f(x)$和$g(x)$有交点的情况,这个时候并不能说谁大谁小。

第二题也很好判断,趋向正无穷的时候很显然是斜渐近线,负无穷水平渐近线。

第三题是一个经典的结论:$\lim_{n \to \infty }\sqrt[n]{a_1^n+a_2^n+…+a_n^n} = max\{a_i\}$,然后就可以转化为分段函数,再根据图像可以很快把B选出来
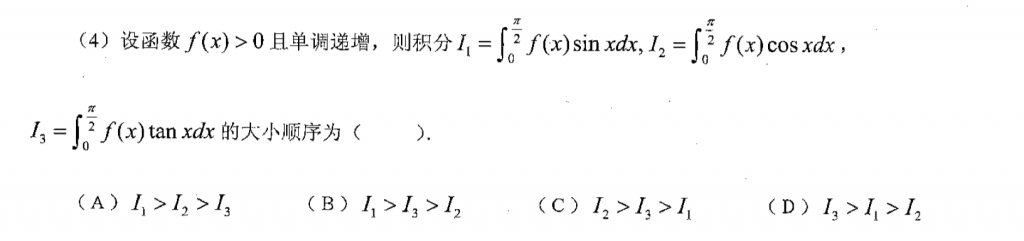
第四题可以用武忠祥讲的图像法,首先可以指定$f(x) = x$,然后根据图像可以知道$I_1>I_2$,然后判断$I_3$的时候就根据$tanx > sinx$和$I_1$比较,就可以判断出来了。
常规的方法是两个函数作差,然后在变号的地方分段,再根据换元法把这两段转换到同一个区间进行比较。

第五题也不难,$B^2-AC<0$,而$A$的正负号没有给定,所以就不能判断是否是极大值还是极小值,C也很好排除,然后D就选出来了。

偏导存在可以推出在十字架是连续的,也就是说:$\lim_{x \to x_0}f(x, y_0) = f(x_0, y_0)$,同理对于$y$的偏导也是如此,就可以推出D了。

这题我做错了,主要是4不太好判断:对于4的判断也是非常厉害的手法:
$$R(A^TA) \le R(A^TA,A^Tb) = R(A^T(A,b)) \le R(A^T) = R(A^TA)$$
然后就能推出$R(A^TA,A^Tb) = R(A^TA)$,方程组一定有解

相似的充要条件肯定就是特征值全部相等了,也就是特征多项式相等

这题可以对分子先变成$e^x$形式,然后用一次拉格朗日把$e$搞掉,然后洛必达就好了

这题简单
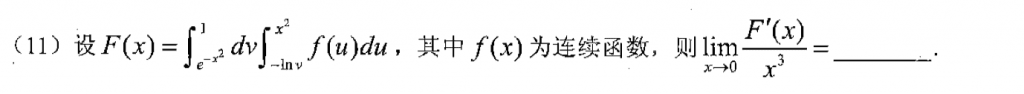
这种题应该一眼洛必达,主要是这个二重积分不能直接求导,需要先交换积分区域

这题要注意是从$(-1, 1)$积分,我给搞成$(0, 1)$了,导致做错
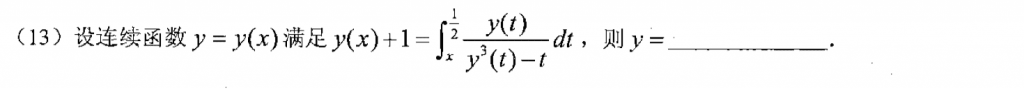
常规题

常规题
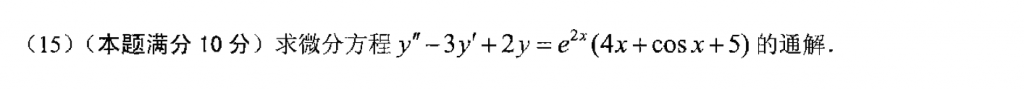
常规题,就是计算要细心,我积分算子法用的不熟练就没有用,用的是最常规的待定系数法,计算量爆炸,有空还是得把积分算子法多练练

这题也不难,直接暴力求导就好了,不用整什么花里胡哨的东西
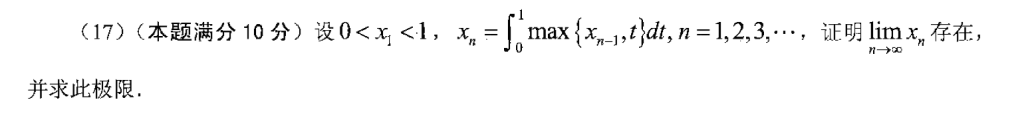
第一眼看到这道题感觉还是挺难的,想了一下就发现是paper tiger了,先用数学归纳法可以把有界性整出来,然后单调性就用后项减前项,对于这个积分,就根据$x_{n-1}$把区间分一下就行。

这题有意思的,先划分区间,因为$[x+y]$在下三角是零,所以下三角就没得了,然后上三角关于y=x对称,用对称性发现被积函数是$ln1$,又没了

当我看到这道题目的时候,这套卷子的满分就是140了

这道题不难,第一问和第二问都用区间再现就好了,对于第二问,我一开始还想把这个m找出来,然后确定哪一部分是$f(x)$,哪一部分是$g(x)$,但是发现整不出来,就直接区间再现了,然后就柳暗花明了。

这道题我想了好久没想出来,还好放弃了,真想不出来。主要是没有往比区间连续函数的那些性质想,比如最大最小值定理,界值定理。然后复盘的时候突然想到了以前汤家凤讲的,见到一系列$f(x)$相加,就要想界值定理!
对于左边的话,要对$f(x)$进行最大最小值放缩,然后$xsinx$的那个积分可以算出来。两边都用界值定理,然后就可以找到两个相等的点了。

这道题也不难,$A(A-2B)=E=(A-2B)A$
第二问就根据第一问的结论,然后A是可逆矩阵,可以消去。

基本题,不说了。







Comments NOTHING