这套试卷是前天做的,结果因为一些原因就拖到了今天,导致有些题目都有些陌生了,以后还是要及时总结,不能拖。客观评价这张卷子,难度和14年第三套相比低了一些,但是计算量还是非常大的,我三个小时做满才写完。
下面开始复盘

第一题难度还好,分子的阶数要么是1,要么是2,如果要是可去间断点的话,那么分母要为一阶,当$b=-1$时,就是传说中的🐶➖sin🐶,那么就是三阶了,其他情况就是一阶,所以就选出来了。
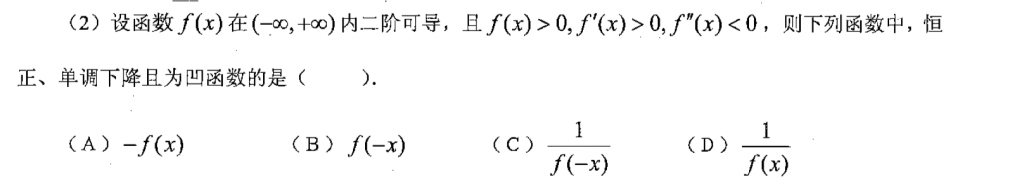
复合函数求导就好了

第三题也不难,左右极限存在,但是左右极限不一定相等,A的话都是右极限,所以没影响,B和C实际上是一样的,都是右极限,而D是的左边是双侧极限,右边是右极限,不匹配。

第四题难的,我蒙了个C给蒙对的,其实这种题的方法都是固定的,主要是这道题迷惑性太强了。首先就是对于这种形式的东西,第一个想法就应该进行区间平移,然后往奇偶性的方向考虑,这道题平移之后,中间过程还需要对n分情况来使用诱导公式,最后可以推出是奇函数,结果就出来了。
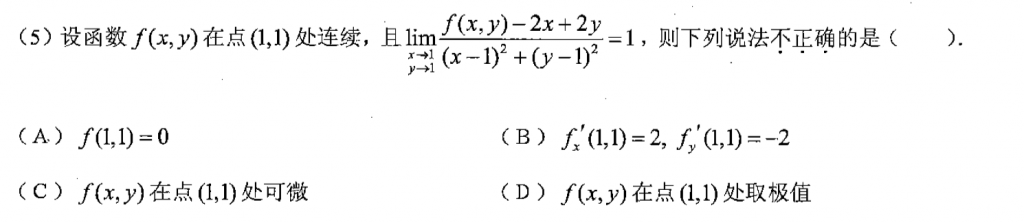
第五题不难,B可以证明是对的,凑微分的定义就行了,然后俩偏导不为零,肯定就不是极值了。
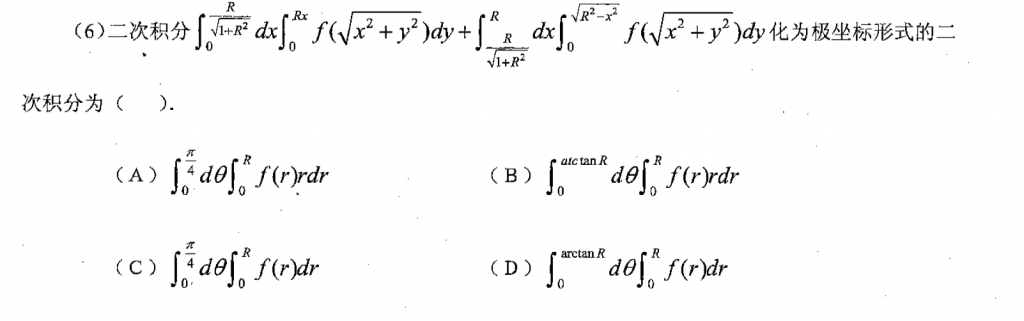
第六题可以很快把答案选出来,CD缺了r肯定不对,然后A的积分区域很好画出来,然后判断不对,B的那个arctan实际上不好推的。

$A^2=0 \to R(A) + R(A) \le 3$,可以把A的秩出来,然后$Ax=b$无关的解向量的个数是$n-r+1$,这是一个结论,可以记忆一下

初等变换,然后两边求逆就好了。

把一个$\frac{1}{x^2}$搞到后面,然后倒代换,就好做了
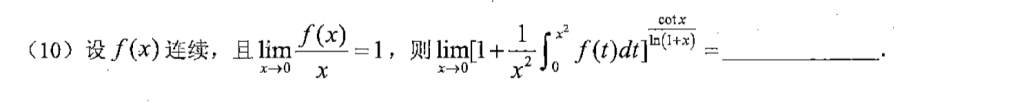
基础题,三部曲简单

这题麻烦的,首先要根据$x$是否大于零或者小于零把$f(x)$作为分段函数求出来,然后再把$lnx$带进去,积分之后,在分段点处要把$C_1, C_2$确定,因为要保证连续。

这题居然还要把a给求出来,我还以为a是固定的。。先把$y'+y=sinx+cosx$的解求出来,然后带C的那一项就是后面那个二阶常系数齐次微分方程的通解,不带C的那一项就是特解,根据通解可以把a给定下来,然后根据特解就可以把$f(x)$确定

这题简单,有一个小trick就是这种填空题的答案一般不会很复杂,如果算的很复杂说明中间估计有什么地方出了问题,可以尝试重新算一下。
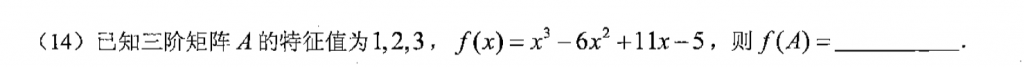
根据A有三个无关的特征向量可以推出$f(A)$也有三个无关的向量,那么肯定是可以对角化的,再根据$f(A)$的三个特征值都是1就可以知道肯定是单位矩阵了。

这题前两问就不说了,第三问的话,答案给的是拉格朗日方法,我这里提供一个方法,由于公式有限就直接用题目的那个条件带了,最好是通分以后,再用一步积分中值定理:
$$\lim_{x\to 0}[\frac{1}{\int_{0}^{x}f(t)dt }-\frac{1}{xf(0)}]=\lim_{x\to 0}[\frac{1}{xf(\xi ) }-\frac{1}{xf(0)}]=\lim_{x\to 0}[\frac{f(0)-f(\xi)}{xf(\xi)f(0)}]=\lim_{x\to 0}[\frac{f(0)-f(\xi)}{\xi-0} \frac{\xi-0}{xf(\xi)f(0)}]=\lim_{x\to 0}[-f'(0)\frac{\xi}{xf^2(0)} ]$$
然后根据第二问的结果,就可以推出要求的极限了。

这题不难,就是算,然后要过原点和在原点处与$x$轴相切可以确定参数

也是算,有一个小trick就是可以先带后求,当然不能一开始就带啊,要把$x$的偏导求出来之后,可以把$x=1$带进去,然后再对$y$求偏导

这题也不难,就是算,我算了好几遍。。计算能力是真不行。
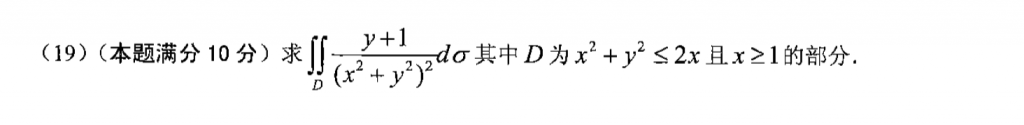
这题可以先用奇偶性把$y$消掉,然后就只剩下$\frac{1}{(x^2+y^2)^2}$了,用极坐标不难算
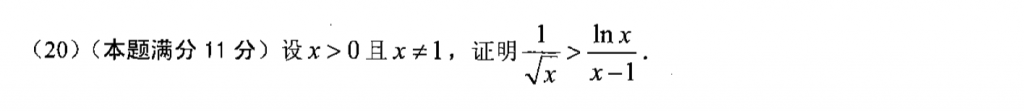
这种题挺灵活的,核心思路就是单调性,但是要怎么构造函数,我感觉试探性挺强的,可能需要经验吧,这题我也做了蛮长时间的,比答案搞的复杂多了。
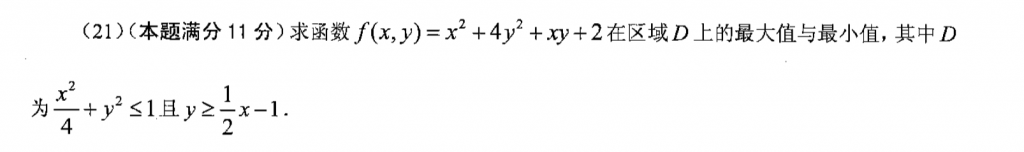
这题我漏了两个点。。答案那个范围我有点没看明白,另外就是目标函数可以用边界函数化简,我没意识到。。也算了挺久的,所以以后用拉格朗日,尤其是这种稍微复杂一些的目标函数,要首先考虑能不能化简。

这题也不难,第一问就白给,第二问的话,先把$Ax=0$的通解带到那个方程里面把a确定下来,这个时候A的解就是B的解了,如果:
$$R(\begin{matrix}
A\\
B
\end{matrix})=R(B)$$ 就可以说明B的解都是A的解
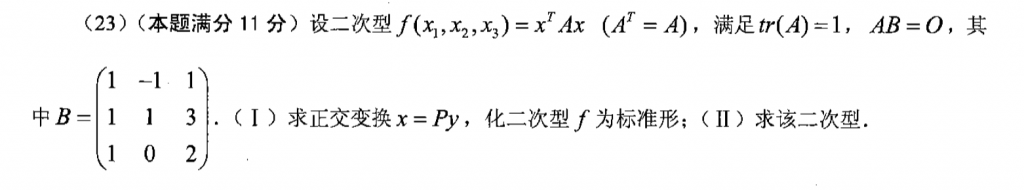
这题挺简单的,首先可以把A的秩给求出来,A是一个秩一矩阵,那么就可以知道A的三个特征值分别是1,0,0,然后标准型就出来了,因为AB=0,那么B的列向量就是Ax=0的解,也就是零特征值对应的特征向量,再根据不同特征值的特征值正交可以求出1特征值对应的特征向量,然后三个特征值,三个特征向量就齐活了,然后就初等变换解吧,初等变换方法我在其他帖子里面写过,这里不重复了。







Comments NOTHING