这套卷子是今天上午做的,依旧是一份高质量的试卷,但是我做的很不好,错的挺多的,下面开始复盘:

第一题我就给做错了,渐近线掉了个垂直的,本来判断间断点的时候我还注意到了$x=-1$是一个无穷间断点,结果没往渐近线那里想,思维局限性太强了。
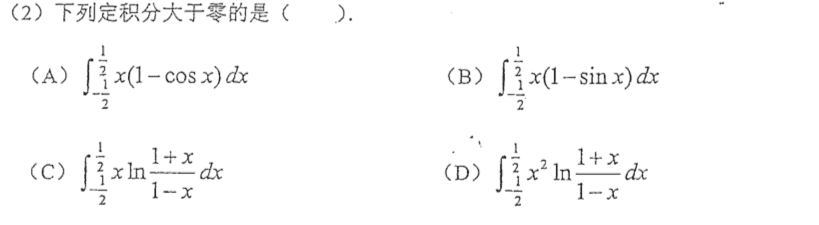
第二题不难,根据奇偶性就可以选出来,要知道那个ln是个奇函数

第三题也不难,我一开始还以为挺麻烦的,然后发现换元:$\sqrt(lnx)=t$之后,这两个积分的积分限就相同了,再用一次分部积分,就可以和后面的那一项抵消掉。

这题我做错了,还以为考的是$y(x)$是周期函数,然后$y'(x),y''(x)$都是周期函数,然后就把B给选了,然后看答案发现还是要求解微分方程或者把特解的形式设出来,看是否为周期。
这种微分方程和周期结合的题目我做过几道,李正元、660高数二阶上都有,但是每次遇到都感觉是非常难的题目,比如下面是李正元的题:

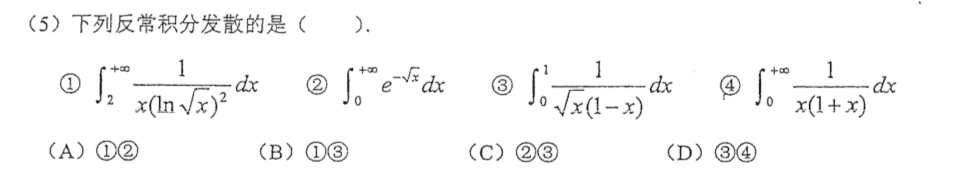
这题我又给做错了。。2很好判断是收敛的,3的话根据1-x的次数是一次也可以很快判断是发散,那么问题就在4,我漏了$x=0$时候的情况,只看到了正无穷,然后以为是收敛的,就直接选了B。。
这题也总结了一个trick,当遇到ln带根号的时候,第一想法是把那个根号给去掉。

这题不难,可以知道$AC-B^2>0, A > 0$,然后就可以推出$A+C > 0$了,当然还有一种情况就是$AC-B^2=0$,其实遇到这种情况,一般都是取不到极值的,所以就可以通过寻找特殊的点或者线来推出不是极值。

这题其实也是基础题,第一个命题和第三个命题都需要这三个向量无关,比方说,在第一个命题中,由于没有说它们是无关的,那么可能里头有一个向量是混子,而Ax=0的基础解系里面无关的向量是两个,那么这三个向量就不可能是基础解系了。
第二个命题和第三个命题实际上就有点解空间的意思了,比如Ax=0的基础解系会支撑起一个空间,那么Ax=0的所有解都在这个空间中,也就是说都可以用它们唯一表示。

这题我感觉也挺难的,其中5是比较好选的,然后4可以通过行变换变成5这是我没想到的。。get
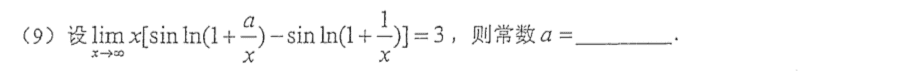
这题我用了两次拉格朗日就出来了,不难
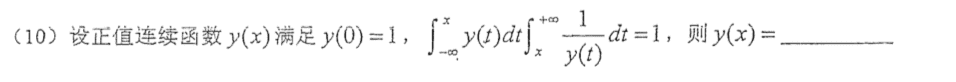
我感觉是挺难的一道题,但是我把答案猜对了hhh,确实没有想到把其中一个移到另一边,然后两边求导,就可以得到微分方程了。

这道题不难,两边求导,然后反函数那个$\varphi(f(lnx+1))=lnx+1$

这种题一般分离参数比较简单,把$e^x$除到左边,然后令$F(x)=\frac{x^2-x-1}{e^x}$,求导分析函数形态,就可以知道a应该怎么取了

形心这玩意数二好像不考,所以我都没怎么看过,知道公式就好了。

$A(\alpha_1, \alpha_2, \alpha_3)$就意识到分块矩阵的乘法了
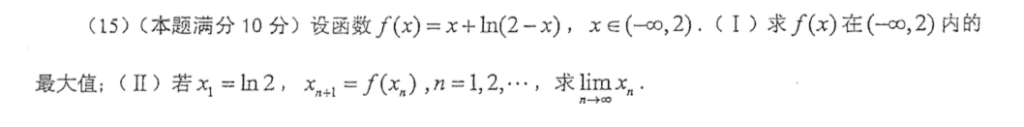
单调有界的简单题,第一问就是有界的提示了,然后第二问那个证明单调就不难了

这题虽然简单,但是第二问要阐述清楚我感觉还是有些麻烦的

分区间求导,又是一道计算量很大的题,耐心算。。

这个题不难,这种化简的题已经做过很多遍了,主要是:$\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}$这样操作

这题也很简单,直接构造函数用单调性是最简单的,答案还用了拉格朗日和柯西,开拓思路还是挺好的。

过过过,怎么老考这种引力
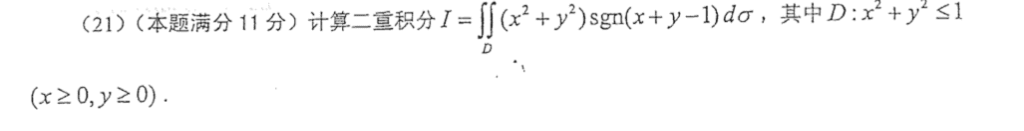
这题也不难,但是我把$x \ge 0, y \ge 0$给看掉了,痛失11分!

这个题比较基础,根据第一行和特征向量的乘积可以知道特征值,然后这三个向量无关就可以推出可以相似对角化。
第二问的话我还把A给算出来了,然后当方程组来做的,太慢了,按照答案的方法两秒钟出结果

这题我没做出来,原来直接把A写出来,然后根据$A\alpha=2\alpha$构造方程,然后把矩阵的元素求出来就好了,我还分析迹什么的分析了半天,硬是搞不出来,就放弃了。
矩阵有了那第二问就简单了。
第三问就是根据特征值全部都大于零,就可以把K的范围搞出来。







Comments NOTHING