这套试卷是今天上午做的,依旧是超越风格,题目难、计算量大,可以很好的模拟在考场上的压力,我觉得平常模拟就是要做这样的卷子!
下面开始复盘:

第一题我就做错了,还以为1是对的。。感觉这种题目就是要多积累一些反例才行,正面推太难想了,超越的答案也没有从正面推,而是每个设问都给了反例。

第二题不难,幂指函数化e就行了

第三题也不难,直接对$I_1$操作就好了,先给它换元:$x=sint$,利用$cos<1$放缩,然后和$I_2$比较。再令$x=tant$,利用$sec>1$放缩,和$I_3$比较。
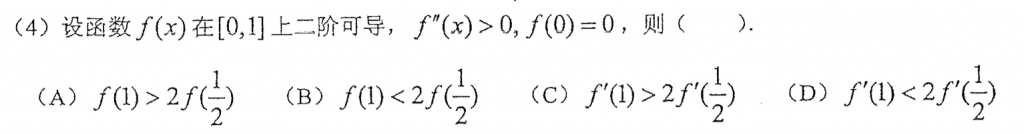
第四题我还真没意识到这是在考凹凸性...这题我直接举的反例,令$f(x)=x^2$,然后就排除bcd了,如果意识到了考察凹凸性,那这道题就非常简单了。

第五题考了个多元函数二阶偏导的概念,但是要注意和一元函数的区分,偏导只和十字架上的点相关,是两条直线,而123都和一个邻域的点相关,是一个面,所以二阶偏导存在只能推一阶偏导存在。

第六题其实2013的超越卷里面出过,基本题

第七题也是一道很有意思的题,知道了基础解系可以推出$R(A) = 3$并且$\alpha_1-2\alpha_2+\alpha_3=0$,这就说明123相关,那么这三个向量中的任意两个向量和4拼在一起肯定就是无关的。
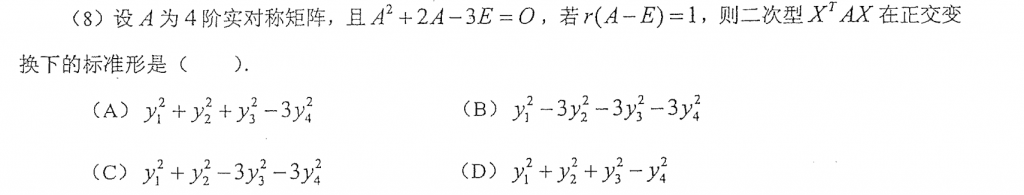
根据给的矩阵方程可以知道矩阵A的特征值只能是1和-3,再根据A-E的秩可以推这俩特征值的个数,然后就出来了。
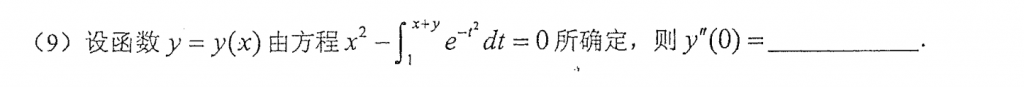
基本题,注意运算就好
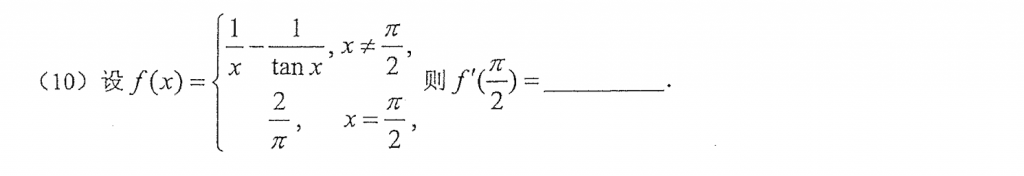
导数定义就出来了
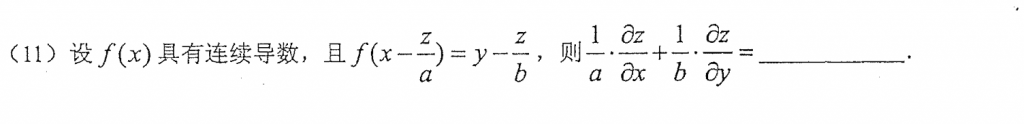
也不难,其实我做这种题喜欢用公式法,两边同时求偏导也是可以的,但是我总感觉还要移项合并同类项啥的,稍微麻烦点,用公式法就很方便。

这题我没做出来,还在想极坐标啥的,走了弯路,直接直角坐标硬算就好了,要相信超越的计算量!

这题也不难,两边除x然后换元:$u=\frac{y}{x}$就可以
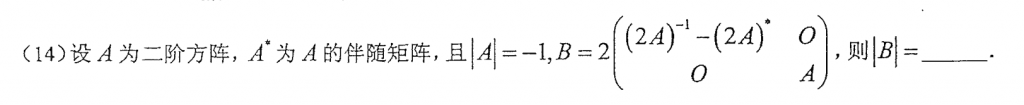
这题我居然做错了,本来还特地想到了B是个四阶矩阵,那么前面的系数2就是2的四次方=16,结果反手写了个4...太粗心了
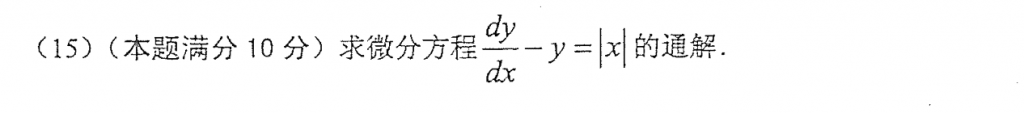
这一问我分了三类,分别是x大于零等于零和小于零,然后再根据连续,确定$C_1, C_2$

这道题还是好证的,就是计算化简麻烦,我搞了十多分钟才算出来,麻了
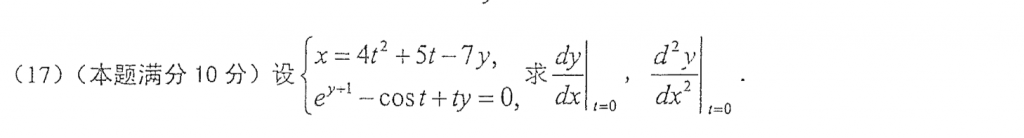
像这种比较麻烦的参数方程我依旧是建议用公式来算,我在其他帖子里面也说过,就是算出$x'(t),y'(t),x''(t),y''(t)$,然后求二阶导数的话就用:$$\frac{y''(t)x'(t)-y'(t)x''(t)}{x'^3(t)}$$
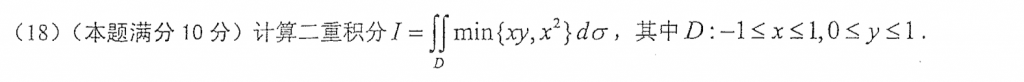
这道题还是有意思的,主要是要分块,在第二象限$xy<0$,那么被积函数肯定就是$xy$了,在第一象限就分块比较$x$和$y$的大小,如果$x$小那就$x$方,如果$y$小那就$xy$。

这道题也不难,没啥思路,但是计算超级烦人,我在计算过程中反复怀疑自己前面是不是有什么地方算错了。。

这题第一问实际上是一个提示,那么第二问就是证明$\varphi (1)=\frac{1}{6}f'(\xi )=\frac{1}{6}\varphi'''(\xi )$,前面那个$\frac{1}{6}$很明显就是泰勒的那个分母的阶乘

第一问的辅助函数其实很好找:$f''(x)+f(x)=2f'(x)\to (f'(x)-f(x))'+(f(x)-f(x))=0$,把$f'(x)-f(x)$看成一个整体就好了,那现在的问题就在于要找两个点让$F(a)=F(b)$,然后用罗尔定理,所以问题就在这个地方,对于构造的辅助函数$F(x)=e^{-x}(f'(x)-f(x))$,我们还需要再次对$f'(x)-f(x)$构造辅助函数:$g(x)=e^{-x}f(x)$,然后现在找三个让$g(x)=0$的点就好了。
第二问就假设有零点,然后推出第一问的结论,和已知条件是矛盾的,这样就可以证明没有零点了。

第22题我感觉是一道很难的题,我没有做出来,我自己也没有什么好的想法,果然这种否定命题的东西用反证法还是比较方便的:

答案的第二问也很精彩,值得学习!

这道题就比较基础了,要先把a给算出来,我一开始还傻乎乎的把a带着算。。感觉不对劲才想到a可以求出来,然后求出第三个特征向量之后单位化就好了,没有难度。







Comments NOTHING