如果说第一套做完感觉还好,那第二套就可以直接抬走了。。三个小时拉满才做了105分,然后考场debuff再减20分,好了,今年可以再次宣布考研失败了。。。
客观评价这张卷子,我的感觉是题目不偏不怪,但是综合性强,计算量大,概念扣的细,考了曲率圆,多元马甲VS一元函数,说实话挺适合模拟的,下面开始复盘了。
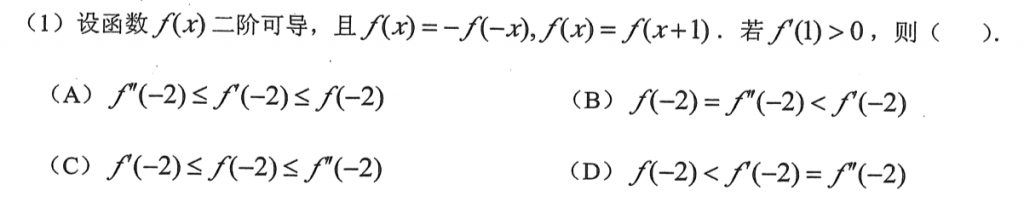
第一题我就做错了,眼睛都看花了,看到f,f',f''还以为要用微分中值定理,搞了几分钟还搞错了,其实挺简单的,f是奇函数,那么f'是偶函数,f''是奇函数,它们都以1为周期,那么就很明显了f(0)=f(-2)=0,f''(0)=f''(-2)=0,然后f'(-2)>0就出来了。

第二题这种题扣概念挺好了,符合现在的趋势,这种题有一个经典的反例就是\(1/x\),然后有界这块有个比较经典的结论,f'(x)在有限区间有界,那么f(x)在这个区间就有界,用拉格朗日可以证,武忠祥强化课讲过证明。所以这道题的C选项实际上就是这个结论的逆否命题。

两类不同函数相乘,尝试分部积分,\(sin^2x\)是很难凑进去的,\(\frac{1}{x^2}\)实际上是好凑的,然后分部积分就好了。

这道题目考了曲率的概念,挺好,正好复习一下,曲线与其对应的曲率圆有相同的切线,而且它们的曲率相同,曲率圆的曲率就是半径的倒数,因此就可以得到f'(0)=0,然后f''(0)=1,就可以得到最后的结果了。

这道题,好!实际上这是一个复合函数,外层的f是一元的!里面的\(x^2+y^2\)是二元的,所以对f求导是不带角标的!

积分区域关于x轴对称,根据y的奇偶性以及在第一象限的积分区域y<x就可以得到结果

这题挺简单的
对于A可以很容易举一个例子,只需要满足A行满秩,比如A=(1, 1, 0),这个时候A动都动不了,所以更不可能化成单位矩阵,右边全零了。
对于B来说,很容易判断是对的,因为R(A|b)=R(A)=m<n,所以一定有无穷多解。
对于C来说,可以取转置,然后\(A^T\)是列满秩,所以只有零解
对于D来说就很容易判断了

A和D很显然都是不对的

这道题我tm做错了,忘记了分母有个3!打草稿的时候一定要保证草稿纸的整洁。其实挺简单的,令xt=u,然后变形求导就好了。

根据奇偶性,然后凑微分,然后换元,令x=sint就好了
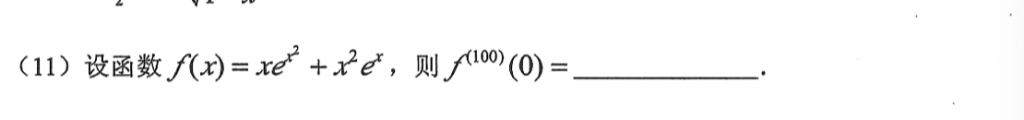
第一项很显然是一个奇函数,那么对它求100次导数之后依旧是奇函数,所以为零,第二项对ex进行泰勒展开,然后\(x^{98}\)前的系数乘100的阶乘就好了。
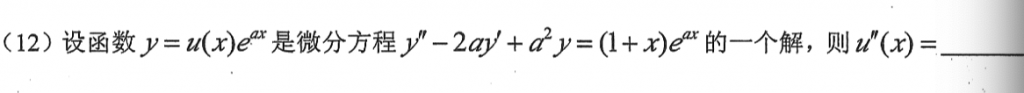
这道题也是很简单的题,直接对y求两次导后带入方程中就出来了,但是我又给算错了 。。
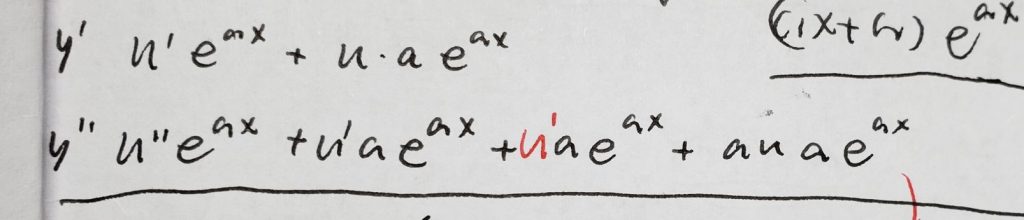
掉了个u',所以导致最后寄了,要细心!

这道题感觉也不难,但是我把图给画错了。。以为是两个圆中间的那个部分,然后就寄了。

直接设A为diag(1, 2, 0),然后就出来了
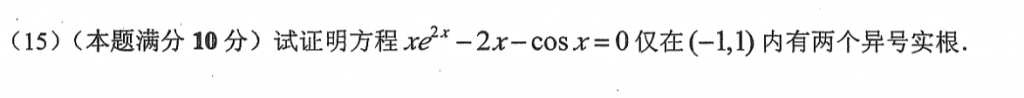
这道题我也没整出来,真菜,虽然不难,但是细节颇多,真有点去年考场上那味了,主要是对这种不太明显的符号判断不太熟悉,需要多做一些题。

第十六题也不难,先把\(l_1, l_2\)表示出来,然后算微分方程就好了,就是计算要细心。

物理题,无力题,跳了跳了
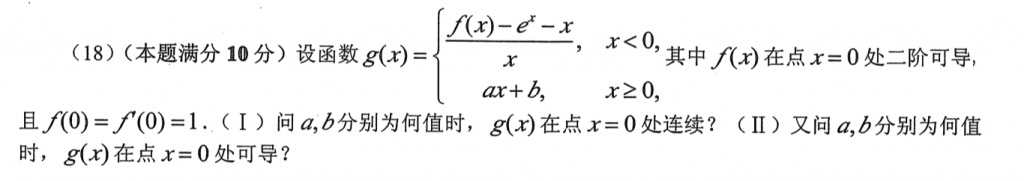
这道题比较基础,就不用多说了。

第一问证明不等式,左边很简单,直接泰勒就好了,右边那个我看了一会,感觉不太好证明,直接写因为f(x)是凹函数,f(x)在0,1弦的下方然后不等式就出来了,不太严谨,凹凸性放缩有空还是需要好好总结。
第二问就很简单了,第一问都给了不等式,第二问直接夹逼就好了。
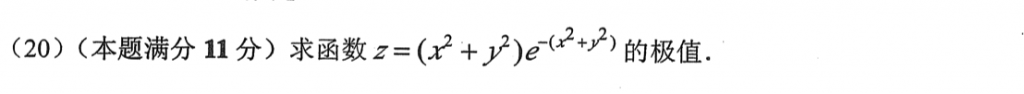
这题是好题,计算量也好大,求出来驻点为(0, 0)和\(x^2+y^2=1\)的点,(0, 0)点的极值点判断直接用AC-B方就好了,计算量好大!然后后面那个可以令\(x^2+y^2=t\),带到z里面,判断t=1是否是极值点。
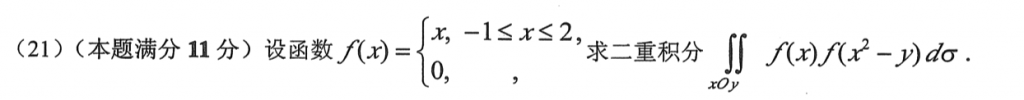
这道题武忠祥辅导讲义上有类似的,先把积分区域确定,然后用f(x)=x把被积函数写出来就好了。

好题,第一问要知道\(A^TAX=0\)和\(AX=0\)同解,第二问就比较常规。

感觉一般,\(A^2\)非正定,那么第三个特征值肯定是零,再根据实对称矩阵不同特征值的特征向量垂直正交就可以把a和第三个特征向量搞出来。求Q就是对这三个特征向量做一个单位化,然后拼起来就好了。







Comments NOTHING