昨天做了一套超越的题,感觉还好,没有想象中那么难,但是题目出的还是挺好的,今天来复盘一下。

第一题就比较基础,铅直渐进线很容易能看出来,斜渐近线也不难,也很容易看出来,如果不放心可以用y/x,然后算两个极限验算一下。

第二题也是很基础的题,根据函数函数的单调性和导数的正负号联系,然后在x=0的地方有垂直渐近线,那么导数就是趋向无穷。
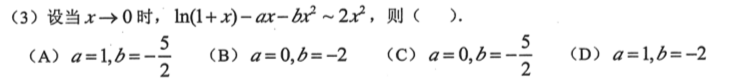
直接泰勒展开就好了,可能很多人不太能记住泰勒公式,这里分享一个记法,\(e^{x}\)应该比较容易记住,然后实际上sin和cos就是一人拿了一半,然后正负交错,ln(x+1)就是去首项,去阶乘,正负交错。

第四题我感觉出的很棒,我的方法不太严谨,先是分区间去掉绝对值,其实这一步就有问题了,然后前后两个都是变限积分,对x求导,再用一个结论,如果F(x)是奇函数,那么F'(x)就是偶函数,反之也成立,然后就推出正确选项了。(验证了一下过程是有问题的)
答案的方法是直接用奇偶定义,然后换元之后就能得到答案了,这个是我没有想到的,可能有些思维定势了,看到这种带绝对值的就会想到拆区间,其实还更麻烦了,算是瞎做做出来的。

这道题出的也挺好的,连续是显然的(但是我脑子不清醒给整错了,以为不连续,然后直接走了一个D。。。)再根据偏导的定义把\(f_x,(0, 0) f_y(0, 0)\)求出来,然后对x求偏导,对y求偏导后判断偏导的连续性即可。

这道题的答案好像给错了,应该是B才对,基础题。

第七题也不难,根据条件实际上可以得到\(\alpha_1,...,\alpha_m\)是线性无关的,m实际上是小于等于n的,所以A和B可以排除,经过一系列的行变换可以把A变成上面是单位矩阵的形式,把下面弄成0,所以D是对的。

第八题也是比较基础的题,记住c是2n✖️2n的就不会错了。

这道题是一道好题,我做错了。。情况没分类好,log这个用一下换底公式:

然后遇到\(ln(\infty )\),总结了一个比较通用的方法,和多项式一样,把最高阶的那一项提出去,然后利用lnab=lna+lnb进行之后的计算
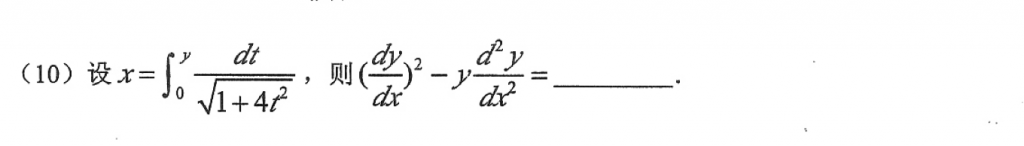
第十题考基础概念考的挺好的,反函数之间的转化要弄的很清楚:\(\frac{dy}{dx}=\frac{1}{\frac{dx}{dy} }\)以及\(\frac{d^2y}{dx^2}=-\frac{x''}{(x^{'})^{3}}\),然后带进去算微分方程就好了,在严选题上做过比较隐晦的这种反函数的微分方程,要自己意识到一个小结构是反函数的二阶导。

这道题和昨天在博客里面复盘的那套卷子里面有道题目挺类似的,根据题目所给的条件可以得到一些点的信息,然后利用分部积分就可以得到结果。

水题,跳了

这道题也挺基础的,一般这种题目有两种做法,第一种是理清变量之间的结构,然后复合函数求导,另一种方法就是使用微分形式的不变形,微分形式不变形我挺容易出错的,但是真香。

这道题也出的挺好的,根据矩阵的秩可以把伴随的秩算出来,然后B*满秩,所以就是求A*的秩。
这里补充一个更加通用的公式对于R(AB),如果A列满秩,那么R(AB)=R(B),如果B行满秩,那么R(AB)=R(A),具体的证明可以用方程解的同解,拿A列满秩的条件来说,实际上是可以证明ABX=0和BX=0同解,那么它们的秩就自然相等了。

不难的题,首先根据条件可以把切线求出来,然后算体积就好了,虽然说二重积分求旋转题的体积挺香的,但是对于一些特别简单的区域来说,直接套公式其实更快,所以在掌握一些比较厉害的方法后,最基本的方法也不能丢。

三部曲+泰勒+看清条件不要乱用洛必达,这题基本就没问题了。

这道题也不难,证明那个公式就拆区间(-a, 0)和(0, a),然后在(-a, 0)这段区间换个元,然后合并就ok了,第第二问用公式计算积分也不难。

这题我居然做错了,淦!好久没碰多元微分了,公式记得不是很扎实......然后就\(\frac{\partial f}{\partial x}(0,0)=-2\)了,导致做错,其实这道题基本是送分题,偏导本质是一元导数,利用定义就可以了。

这道题好像和22那道真题挺像的,时间过去太久了我也记不太清了,考场上那道题我算错了,看着简单,我感觉其实挺麻烦的。这道题就比较简单了,极坐标就出来了,但是我还是搞错了,错的还挺离谱的:

我做题真的挺粗心的,得好好好好改改。

这道题挺有意思的,题目给的那个积分不等式我第一次遇到的时候也挺懵逼的,在武忠祥的严选题上的中值定理部分遇到过,然后积累下来了,把那个\(\frac{1}{2}\)可以移到左边,然后凑到积分里面去,被积函数就变成了f(x)+x,然后用一个积分中值定理就就可以得到存在点小于零。
然后对于后面的那个极限,我用了个东西:\(\lim_{x \to \infty }\frac{f(x)}{x} =\frac{f(x)}{x}+\alpha\),然后就可以证明存在点,让\(f(x)+x>0\)了,这种比较概念的题还是有些麻烦的,去年的选择题来了波概念,今年的大题说不定也会搞一波概念,得防一手。

这题没啥难度,就是纯模拟,严选题上这种题目挺多的,还比这个难,严选上我记得比较清楚的是有些题目需要换元才能积出来,比如y方啥的,这个直接其次就好了。

这道题目的第一问主要还是围绕秩来考察,很显然,R(PA)=R(A)=R(C)=2,再根据R(A)+R(B)<=3,得到B的秩为1,K就出来了,因为PA=C,也就是说对A做一系列的行变换可以变成C,然后直接对C操作,C的第一列和第三列是无关的,可以说明A的第一列和第三列无关,再根据B的列向量是Ax=0的解,可以得到线性组合的系数。

这道题也挺经典的,第一问就是把\(\beta\)写开,然后用特征值特征向量的定义+分块矩阵乘法把这个向量组写成\(\alpha_1, \alpha_2, \alpha_3\)和一个矩阵相乘,而\(\alpha_1, \alpha_2, \alpha_3\)是无关的,因此只需要算出来后面的那个矩阵行列式不等于零就行了。
第二问给了A的三次方,所以可以给\(\beta, A\beta, A^2\beta\)乘一个A,然后变形,再用分块矩阵的乘法就可以把P矩阵写出来,然后\(P^{-1}AP=B\)
第三问要证明\((A^2-2E)x=0\),一般这种相似的东西,会用另一个矩阵来算,比如这里的A我们并不知道,但是我们知道B,所以就可以尝试把问题转换为\((B^2-2E)x=0\),首先把秩给算出来,看基础解系的个数,然后尝试证明\(A\beta\)和\(A^2\beta\)是这个方程的两个解,因为第一问已经证明过了它们是无关的,所以它们是基础解系,然后通解就出来了。







Comments NOTHING