图的基本结构和基本操作

最近一直在研究严书风格的图代码，感觉比之前学习算法时用的“前向星”的操作要麻烦一些，不过总算是有点小突破。现在以王道P211练习题的第四题入手，来实现一下图的邻接表以及如何在这个存储结构上跑DFS。

头文件以及一些预定义

#include<iostream>
using namespace std;

#define MaxVertexNum 100
#define VertexType char

图的结构主要包含两个部分：第一个部分是边表（画红框部分），类似链表，主要包含一个结点的编号（也就是数字序列），另一个是指向下一个边表结点的指针

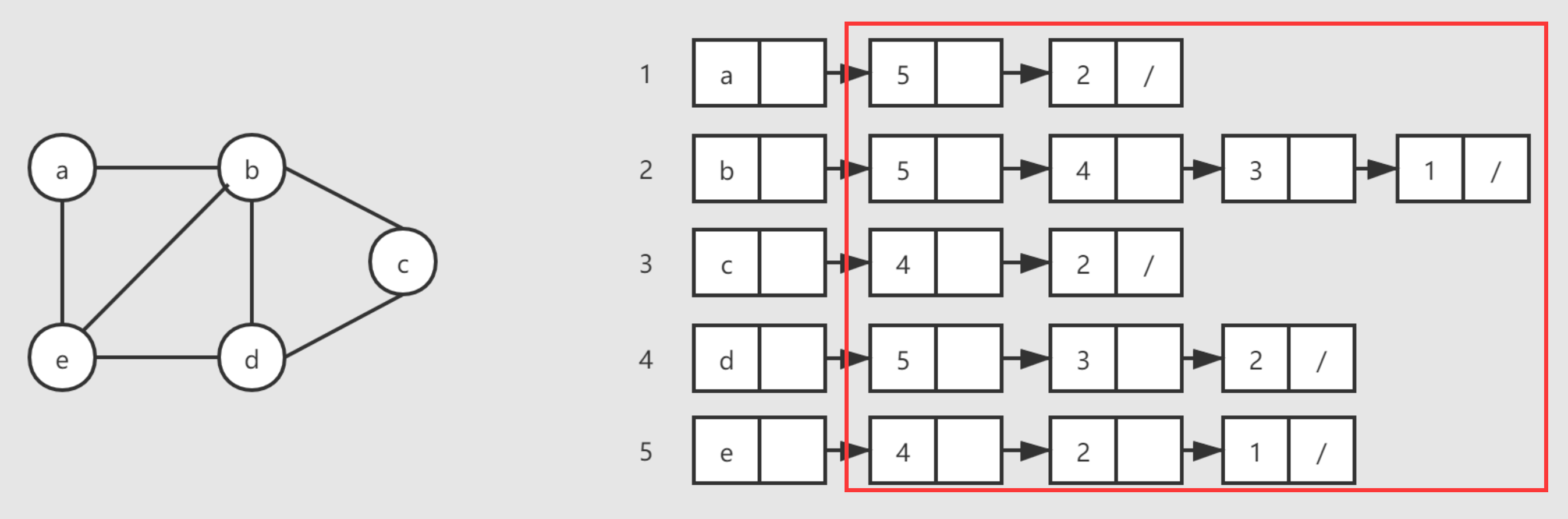
typedef struct ArcNode { 
    int adjvex;          //结点的编号
    ArcNode * next;      //指向下一个边表
}ArcNode; // 边表

第二个部分是顶点表，顶点表用一个数组AdjList将顶点存起来，其中的每个顶点主要由两部分组成，一个是顶点的值（也就是字符表示），另一个是指向边表的指针，也就是说，顶点表中存放的结点其实就相当于边表的头节点。

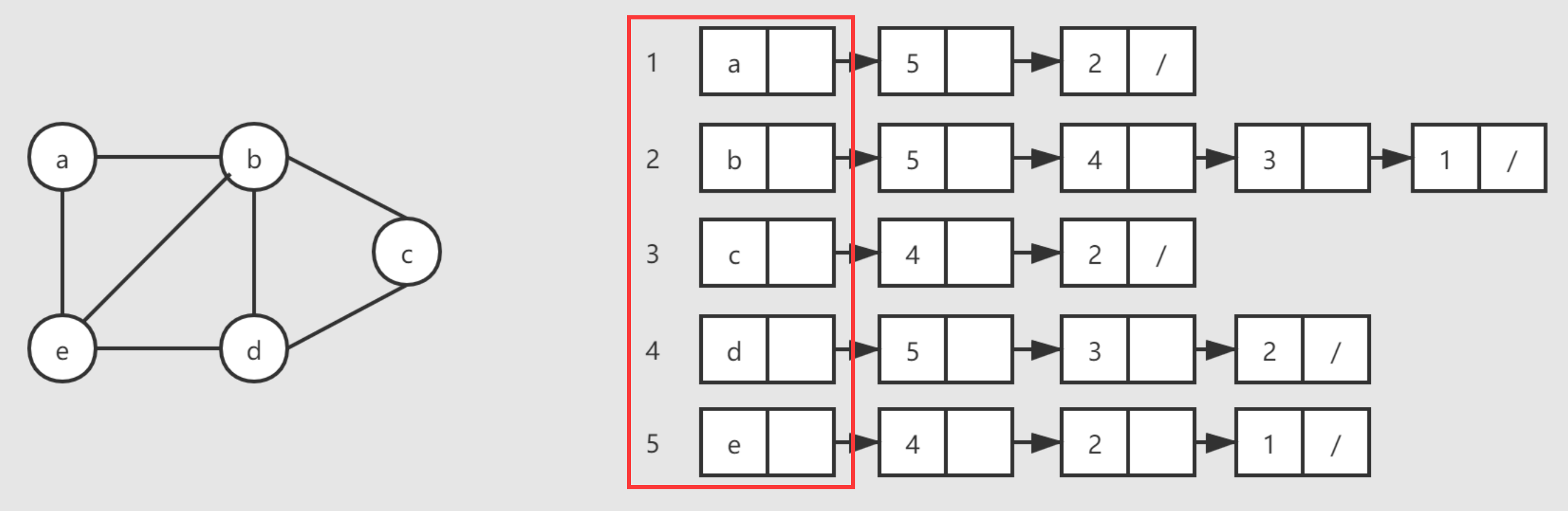
//顶点表结点
typedef struct VNode {  
    VertexType data;            //顶点的值
    ArcNode * first;              //指向边表
} VNode, AdjList[MaxVertexNum]; //顶点和顶点表

最后再使用一个结构体存放顶点表和图的顶点数和边数

//图的存储结构
typedef struct {       
    AdjList vertices;    //邻接表，用于存放结点的值，其下标就是结点的编号
    int vertexnum, arcnum; //维护图的顶点数和边的个数
} ALGraph;

这里有一个细节就是使用typedef来定义一个数组，大家可能之前没有用过或者用的很少，这里举个简单的例子，比方说typedef int vector[10]; 这条语句定义了一个元素类型为int，含有10个元素的数组类型vector，之后要使用的时候：vector v1,v2; 这就定义了两个数组v1和v2，每个数组都包含十个int类型的元素。这里定义的AdjList vertices也是如此，它是一个数组，用于存放顶点，数组长度为MaxVertexNum。

LocateVex操作，用于根据顶点的值（字符），找到其编号（数字序列，在vertices中的位置（下标），在边表中是adjvex）

//找到结点x在顶点表中的位置
int LocateVex(ALGraph & G, VertexType x) {
    for(int i = 0; i < G.vertexnum; i ++) {
        if(x == G.vertices[i].data) 
            return i;
    }
    return -1;
}

之后比较麻烦的就是图的创建了，这块看看我写的注释应该可以看懂

大概流程：输入节点数和边数，然后输入每个结点的值，之后输入边，每输入一条边（两个结点的值）都需要先通过LocateVex找到对应的结点编号，然后使用类似头插法的操作，将这个结点作为边表结点插入到对应的顶点后面，因为是无向图，所以需要两次建边，比如（a, b），需要先 a -> b，再b -> a。

void CreateALGrapha(ALGraph & G) {
    cout << "输入顶点数和边数：";
    cin >> G.vertexnum >> G.arcnum;
    for(int i = 0; i < G.vertexnum; ++i) {
        cout << "输入第" << i + 1 << "个顶点的信息：";
        cin >> G.vertices[i].data;        //将结点的值保存到vertices
        G.vertices[i].first = NULL;       //这里一定要初始化一下
    }

    for(int i = 0; i < G.arcnum; ++i) {
        VertexType e1, e2;
        cout << "输入第" << i + 1 << "条边的顶点：";  //一条边需要两个结点确定
        cin >> e1 >> e2;           
        ArcNode * e = new ArcNode;        //用malloc也行
        if(!e) {
            cout << "内存分配失败：" << endl;
            exit(0);
        }
        
        int vi = LocateVex(G, e1);    //根据值找到编号
        int vj = LocateVex(G, e2);

        //e1和e2之间有一条边，类似头插法将e2的边表结点插到e1的顶点表后
        e -> adjvex = vj;
        e -> next = G.vertices[vi].first;
        G.vertices[vi].first = e;
	
	//无向图需要插入两次，将e1的边表结点插到e2的顶点表后
        e = new ArcNode;
        if(!e) {
            cout << "内存分配失败：" << endl;
            exit(0);
        }
        
        //再将e1的边表插到e2的顶点表
        e -> adjvex = vi;
        e -> next = G.vertices[vj].first;
        G.vertices[vj].first = e;
    }
}

创建好了之后，跑下DFS

DFS每次会以编号为i的结点为起点搜索一个连通块，也就是说，调用dfs的次数，取决于连通块的个数。

DFSTraverse，则是对每个结点都跑一下DFS，因为图可能不连通

bool visited[MaxVertexNum];
//邻接表从起点i开始的深度优先搜索
void DFS(ALGraph G, int i) { 
    ArcNode * p;
    cout << G.vertices[i].data << endl;  
    visited[i] = true;       //标记当前结点为访问过
    p = G.vertices[i].first;   //p指向当前顶点相邻的边表
    while(p) {
        if(!visited[p -> adjvex]) {   //如果还没有访问过，那就访问
            DFS(G, p -> adjvex);
        }
        p = p -> next;     //看看下一个结点
    }
}

//邻接表的全局深度优先搜索
void DFSTraverse(ALGraph G) {
    for(int i = 0; i < G.vertexnum; ++i){   //初始化visit数组为false
        visited[i] = false;
    }

    for(int i = 0; i < G.vertexnum; ++i) {  //不一定是连通图，所以每个结点都要看看
        if(!visited[i])
            DFS(G, i);
    }
}

全部代码

#include<iostream>
using namespace std;

#define MaxVertexNum 100
#define VertexType char

//边表结点
typedef struct ArcNode { 
    int adjvex;          //存储该结点在顶点表中的下标
    ArcNode * next;      //指向下一个边表
}ArcNode;

//顶点表结点
typedef struct VNode {  
    VertexType data;            //顶点信息
    ArcNode * first;             //指向边表
} VNode, AdjList[MaxVertexNum]; //顶点和顶点表

//图的存储结构
typedef struct {       
    AdjList vertices;  //邻接表
    int vertexnum, arcnum; //维护图的顶点数和边的个数
} ALGraph;

//找到结点x在顶点表中的位置
int LocateVex(ALGraph & G, VertexType x) {
    for(int i = 0; i < G.vertexnum; i ++) {
        if(x == G.vertices[i].data) 
            return i;
    }
    return -1;
}

void CreateALGrapha(ALGraph & G) {
    cout << "输入顶点数和边数：";
    cin >> G.vertexnum >> G.arcnum;
    for(int i = 0; i < G.vertexnum; ++i) {
        cout << "输入第" << i + 1 << "个顶点的信息：";
        cin >> G.vertices[i].data;
        G.vertices[i].first = NULL;
    }

    for(int i = 0; i < G.arcnum; ++i) {
        VertexType e1, e2;
        cout << "输入第" << i + 1 << "条边的顶点：";
        cin >> e1 >> e2;
        ArcNode * e = new ArcNode;
        if(!e) {
            cout << "内存分配失败：" << endl;
            exit(0);
        }

        
        int vi = LocateVex(G, e1);
        int vj = LocateVex(G, e2);

        //e1和e2之间有一条边，先用头插法将e2的边表插到e1的顶点表后
        e -> adjvex = vj;
        e -> next = G.vertices[vi].first;
        G.vertices[vi].first = e;

        e = new ArcNode;
        if(!e) {
            cout << "内存分配失败：" << endl;
            exit(0);
        }
        //再将e1的边表插到e2的顶点表
        e -> adjvex = vi;
        e -> next = G.vertices[vj].first;
        G.vertices[vj].first = e;
    }
}

bool visited[MaxVertexNum];
//邻接表从起点i开始的深度优先搜索
void DFS(ALGraph G, int i) {  //DFS每次会搜索一个连通图，也就是说，调用dfs的次数，取决于连通块的个数
    ArcNode * p;
    visited[i] = true;
    cout << G.vertices[i].data << endl;
    p = G.vertices[i].first;
    while(p) {
        if(!visited[p -> adjvex]) {
            DFS(G, p -> adjvex);
        }
        p = p -> next;
    }
}

//邻接表的全局深度优先搜索
void DFSTraverse(ALGraph G) {
    for(int i = 0; i < G.vertexnum; ++i){
        visited[i] = false;
    }

    for(int i = 0; i < G.vertexnum; ++i) {
        if(!visited[i])
            DFS(G, i);
    }
}

int main() {
    ALGraph G;
    CreateALGrapha(G);
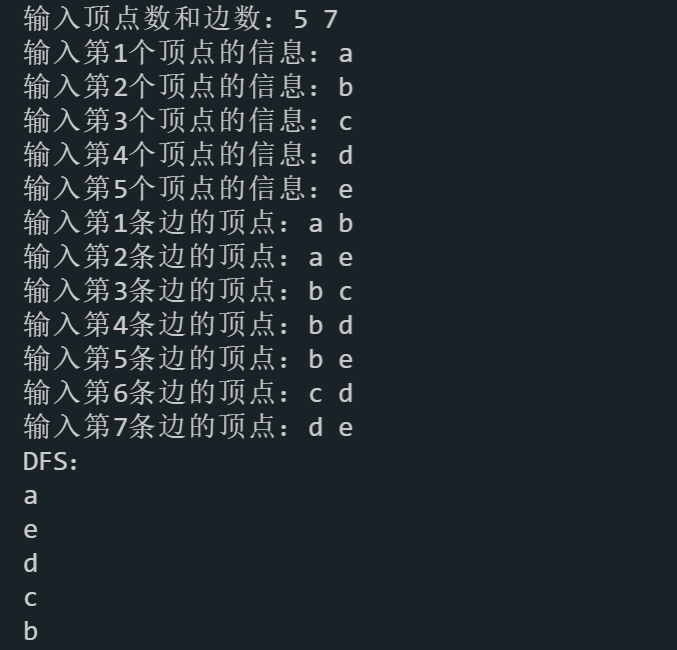
    cout << "DFS：" << endl;
    DFSTraverse(G);  
}

/*
以图一为例的输入序列
输入序列
5 7
a b c d e
a b
a e
b c
b d
b e
c d
d e
*/

邻接表to邻接矩阵

其实思路很简单，就是遍历每个顶点的邻接表，因为邻接表结点中存放的正是顶点的相邻结点的编号，在数组的对应位置修改为1，思路很简单，但是前提是要对图的存储结构比较熟悉。

int Matrix[MaxVertexNum][MaxVertexNum];
void Table2Matrix(ALGraph G) {
    for(int i = 0; i < G.vertexnum; ++i) {  //访问每个顶点
        ArcNode * p = G.vertices[i].first;    //遍历顶点的邻接表
        while(p) {
            Matrix[i][p -> adjvex] = 1;          //将对应位置修改为1
            p = p -> next;
        }
    }
}

完整代码

#include<iostream>
using namespace std;

#define MaxVertexNum 100
#define VertexType char

//边表结点
typedef struct ArcNode { 
    int adjvex;          //存储该结点在顶点表中的下标
    ArcNode * next;      //指向下一个边表
}ArcNode;

//顶点表结点
typedef struct VNode {  
    VertexType data;            //顶点信息
    ArcNode * first;             //指向边表
} VNode, AdjList[MaxVertexNum]; //顶点和顶点表

//图的存储结构
typedef struct {       
    AdjList vertices;  //邻接表
    int vertexnum, arcnum; //维护图的顶点数和边的个数
} ALGraph;


//找到结点x在顶点表中的位置
int LocateVex(ALGraph & G, VertexType x) {
    for(int i = 0; i < G.vertexnum; i ++) {
        if(x == G.vertices[i].data) 
            return i;
    }
    return -1;
}

void CreateALGrapha(ALGraph & G) {
    //cout << "输入顶点数和边数：";
    cin >> G.vertexnum >> G.arcnum;
    for(int i = 0; i < G.vertexnum; ++i) {
        //cout << "输入第" << i + 1 << "个顶点的信息：";
        cin >> G.vertices[i].data;
        G.vertices[i].first = NULL;
    }

    for(int i = 0; i < G.arcnum; ++i) {
        VertexType e1, e2;
        //cout << "输入第" << i + 1 << "条边的顶点：";
        cin >> e1 >> e2;
        ArcNode * e = new ArcNode;
        if(!e) {
            cout << "内存分配失败：" << endl;
            exit(0);
        }
        
        int vi = LocateVex(G, e1);
        int vj = LocateVex(G, e2);

        //e1和e2之间有一条边，先用头插法将e2的边表插到e1的顶点表后
        e -> adjvex = vj;
        e -> next = G.vertices[vi].first;
        G.vertices[vi].first = e;
		
        e = new ArcNode;
        if(!e) {
            cout << "内存分配失败：" << endl;
            exit(0);
        }
        
        //再将e1的边表插到e2的顶点表
        e -> adjvex = vi;
        e -> next = G.vertices[vj].first;
        G.vertices[vj].first = e;
    }
}

int Matrix[MaxVertexNum][MaxVertexNum];
void Table2Matrix(ALGraph G) {
    for(int i = 0; i < G.vertexnum; ++i) {
        ArcNode * p = G.vertices[i].first;
        while(p) {
            Matrix[i][p -> adjvex] = 1;
            p = p -> next;
        }
    }
}

int main() {
    ALGraph G;
    CreateALGrapha(G);
    Table2Matrix(G);
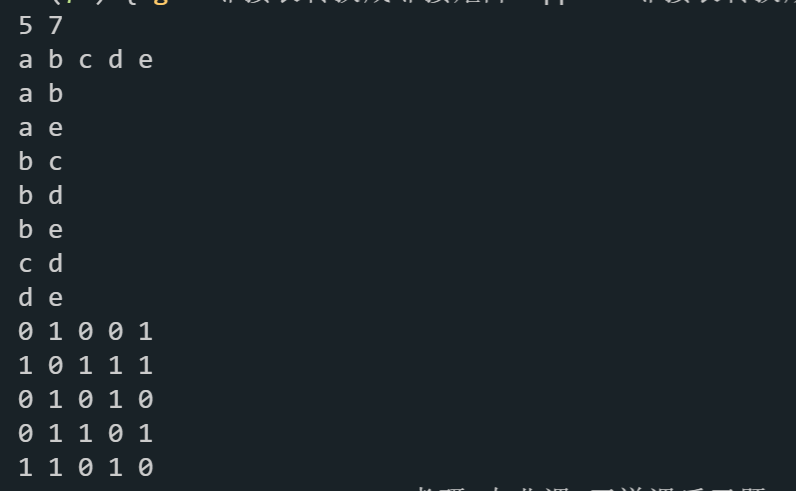
    for(int i = 0; i < G.vertexnum; ++i) {
        for(int j = 0; j < G.vertexnum; ++j) {
            cout << Matrix[i][j] << " ";
        }
        cout << endl;
    }
    return 0;
}

/*
5 7
a b c d e
a b
a e
b c
b d
b e
c d
d e
*/

图的结构+创建+邻接表转换成邻接矩阵（严书风格代码）

图的基本结构和基本操作

邻接表to邻接矩阵

考研八月复习总结

队列+图的BFS（严书风格代码）

vsbf

Comments | NOTHING

取消回复