编译
先给出编译的简要概念:专指由高级语言转换为低级语言。
编译阶段主要分为三个阶段:编译——汇编——运行
- 在编译时:编译器将源程序通过编译程序转换成汇编语言
- 在汇编时:编译器将汇编语言通过汇编程序转换成目标代码
- 在运行时:初始数据会通过目标代码运行子程序然后计算结果
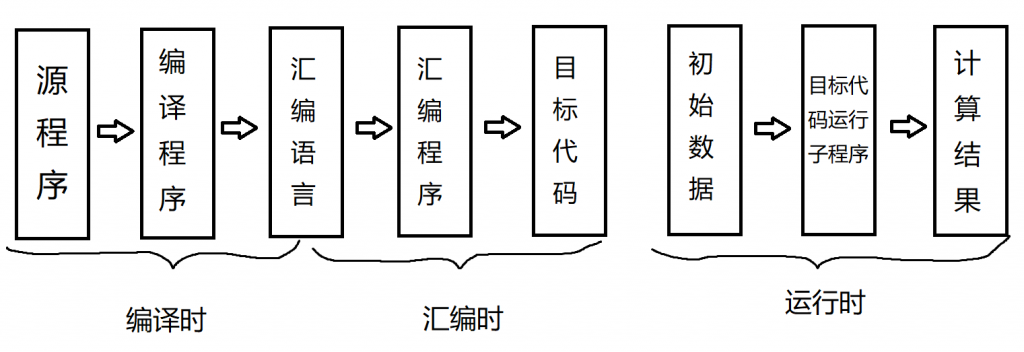
在编译原理这门课中,我们主要研究的就是编译程序的过程,编译程序的工作一般有如下步骤:
- 词法分析
- 语法分析
- 语义分析和中间代码生成
- 优化
- 目标代码生成
具体的每个内容,我以后会写在博客中,下面来聊一聊语法这个东西。
语法
对于高级语言来讲,其实程序语言就是一个记号系统,其主要分为语法和语义,而语法是用来起约束作用的。
任何语言程序都可以看成是一定字符集上的字符串,而语法使得这串字符形成一个形式上正确的程序,这句话其实很好理解,比如在英语中,我们通过语法连词成句,使其形成一个形式上正确的句子。
所以可以看出,语法其实是由词法规则和语法规则组成的,比如0.5 * x1 + c,其中0.5, x1, c, *,+是语言的单词符号,而0.5 * x1 + c是语言的语法单位。
语法组成:
- 单词符号:也就是语言中具有独立意义的最基本结构
- 词法规则:词法规则规定了字母表中哪些字符串是单词符号; 单词符号一般包括常数、标识符、基本字、算符、界限符等。
- 语法单位:也就是一些语法
- 语法规则:语法规则规定了如何从单词符号来形成语法单位;语法规则一般由表达式、子句、语句、函数、过程、程序构成
语言的词法规则和语法规则定义了程序的形式结构,是判断输入字符串是否构成一个形式上正确的程序的依据。
了解一下字母表和符号串
还是先看看一堆概念:
- 字母表:是符号的非空有穷集合,用\(\Sigma\)、\(V\)表示
- 符号:语言中最基本的不可再分的单位
- 符号串:字母表中符号组成的又穷序列,空串比较特殊,表示不含有任何富豪的串称为空串,记作\(\varepsilon\)
- 句子:字母表上符合某种规则构成的串
- 语言:字母表上句子的集合
- Note:一般用\(a\), \(b\), \(c\)来表示符号,用\(\alpha\),\(\beta\),\(\gamma\)表示符号串,用\(A\), \(B\), \(C\)表示其集合
在符号串集合上的一些运算:
- 连接运算,也叫乘积运算,其定义如下:若串集\(A=\left\{ \alpha _1,\alpha _2,\cdots \right\}\),串集\(B=\left\{ \beta _1,\beta _2,\cdots \right\}\),则称乘积\(AB=\left\{ \alpha \beta | \alpha \in A\,\,and\,\,\beta \in B \right\}\)
- 串集自身的乘积乘坐串集的方幂
- \(A^0=\left\{ \varepsilon \right\}\)
- 字母表\(A\)的\(n\)次方幂是字母表\(A\)上的所有长度为\(n\)的串集
- 闭包运算,也叫星闭包:\(A^*\):\(A^*=A^0\cup A^1\cup \cdots\),也就是由\(A\)上符号组成的所有串的集合(包括空串)
- 正闭包运算:\(A^+=A^1\cup A^2\cup \cdots =A^*-\left\{ \varepsilon \right\}\),由\(A\)上符号组成的所有串的集合,当然,不包括空串
- 语言:是字母表上符合某种规则的语句组成的,而字母表上的语言,就是字母表上正闭包的子集
文法
文法就是描述语言的语法结构的形式规则,这样定义非常抽象,我们来看个栗子:
加入我们由这样的一个例子:Young men like pop music.
英语语法规则大家应该都懂:

而文法其实就是上面的这些东西,也就是一些语法结构的一些规则,然后将其形式化了。
文法的一些概念
一个文法一般是由如下东西组成的:\(G=\left( V_N, V_T, P, S \right)\),也就是一个四元组,其中
- \(G\),就是\(grammer\),表示文法
- \(V_N\):\(nonterminal - variable\),表示非终结符集合,一般出现在规则的左部,用<>括起来,表示一定语法概念的次
- \(V_T\):\(terminal - variable\),表示终结符集合,语言中不可再分割的字符串
- \(P\):\(production\),表示产生式集合,用来定义符号串之间关系的一组规则
- \(S\):\(start\),起始符号集合,表示所定义的语法范畴的非终结符
还有一些什么推导和规约的概念非常简单,这里就不再详述了,有个地方要解释一下就是最左推导和最右推导,最左规约和最右规约
- 最左(右)推导:每次使用一个规则,以其右部取代符号串最左(右)的非终结符
- 最左(右)规约:是最右(左)推导的逆过程
- Note:最左推导和最右推导称为规范推导,最左规约称为规范规约
句子, 句型和语言:
- 句型:从文法的开始符号S开始,每步推导所得到的字符串\(\alpha\),记作:\(S\overset{*}{\rightarrow}\alpha\),其中\(\alpha \in \left( V_N\cup V_T \right) ^*\),通俗的讲就是在推导过程中出现的式子都叫句型
- 句子:仅含终结符的句型
- 语言:语言是由\(S\)开始,通过1步或者1步以上的推导所得到的句子的集合,记作:\(L\left( G \right) =\left\{ \alpha |S\overset{+}{\rightarrow}\alpha , \text\{且\}\alpha \in V_T* \right\}\)
文法的分类
Chomsky对文法施加的限制,可分为四类:0型文法,1型文法,2型文法,3型文法,下面我们分别来对每一类文法进行介绍:
- 0型文法(短语文法或无限制文法):
- \(P\)中产生式\(\alpha \rightarrow \beta\),其中\(\alpha\)中至少有一个符号(\(\alpha \in V^+\)),并且至少含有一个非终结符,而不对\(\beta\)作任何要求:\(\beta \in V^*\),总的来说就是对左边要求有一个非终结符
- 识别0型语言的自动机称为图灵机
- 0型语言是对产生式限制最少的文法
- 任何0型语言都是递归可枚举的
- 对0型文法产生的形式作某些限制,可得到其他类型的文法的定义
- 1型文法(上下文有关文法或长度增加文法)
- \(P\)中产生式\(\alpha \rightarrow \beta\),除可能有开始符号产生空串(\(S \rightarrow \varepsilon\))外均有右边长度大于左边长度(\(|\beta |\geqslant |\alpha |\)),若有(\(S \rightarrow \varepsilon\)),则规定S不得出现在产生式的右部
- 或者,\(P\)中产生式\(\alpha \rightarrow \beta\),出可能有开始符号产生空串外,均有\(\alpha A\beta \rightarrow \alpha \gamma \beta\),其中\(\alpha ,\beta \in V^*, A\in V_N,\gamma \in V^+\),也就是说\(A\)这个非终结符,在前面是\(\alpha\),后面是\(\beta\)的条件下,可以变成\(\gamma\),而\(\gamma\)不能为空,所以其长度必然是大于等于1的,也就是大于等于A,这就和上面的定义相呼应了。
- 识别1型文法的自动机称为线性界限自动机(LBA)
- 1型文法意味着,对非终结符进行替换时务必考虑上下文,并且,一般不允许替换成\(varepsilon\),除非是开始符号产生\(varepsilon\)
- 2型文法(上下文无关文法)
- \(P\)中产生式具有形式:\(A \rightarrow B\),其中\(A \in V_N, \beta \in V^*\)
- 也就是说,2型文法对产生式的要求是:产生式左部一定是非终结符,产生式右部可以是终结符、非终结符和空串,非终结符的替换,不必考虑上下文。
- 识别2型语言的自动机称为下推自动机
- 3型文法(正则文法、右线性文法或左线性文法)
- \(P\)中产生式具有形式\(A \rightarrow \alpha B, A \rightarrow \alpha\)(右线性),或者\(A \rightarrow B\alpha, A \rightarrow \alpha\)(左线性),其中\(A, B \in V_N, \alpha \in V_T^*\)
- 也就是说,一个非终结符要么产生一个终结符,要么产生一个终结符后面跟一个非终结符,这个就叫做右线性文法,或者要么产生一个终结符,要么产生一个非终结符后面跟一个终结符,这个就叫做左线性文法
- 3型文法中的产生式要么均是右线性产生式,要么均是左线性产生式,不能既有左线性产生式,又有右线性产生式,若所有产生式都为左线性产生式,则称其为左线性文法,否则为右线性文法
- 识别3型语言的自动机称为有限状态自动机
以上就是对各类文法的一些简单介绍,可以看出,这些文法是逐级限制,逐级包含的,下面的图很清楚的可以表达这个意思:
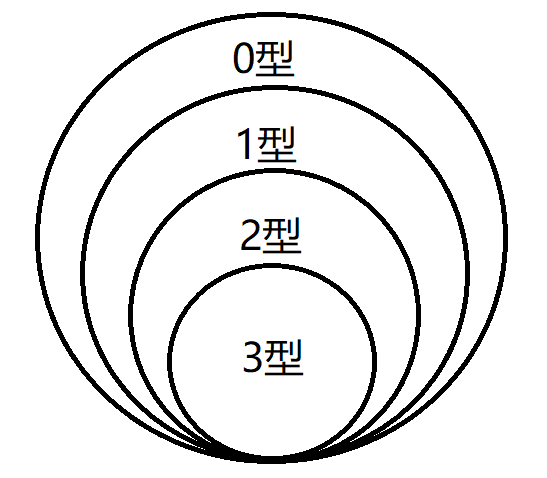
也就是说,如果一个文法是3型文法,那么你也可以说他满足0型文法、1型文法、2型文法,都是可以的。
我在这里只是简单的介绍了各类文法,这几类文法都比较抽象,刚开始看不懂很正常的,最好结合着书上的例子来研究。
文法与语言
所谓的语言,比如i型语言,起始就是由i型文法生成的语言,称为i型语言,记为:\(L\left( G \right) :L\left( G \right) =\left\{ w|w\in V_{T}^{*}, \text{且}S\overset{+}{\rightarrow}w \right\}\)
有一类题目:根据文法推语言:
eg.1 设文法\(G_1=\left( \left\{ S \right\} ,\left\{ a, b \right\} , P, S \right)\),其中\(P\)为:(0)S->aS (1)S->a (2)S->b
简单分析一下可以知道,S最终肯定会以a或者b结尾,所以只需要考虑前面:
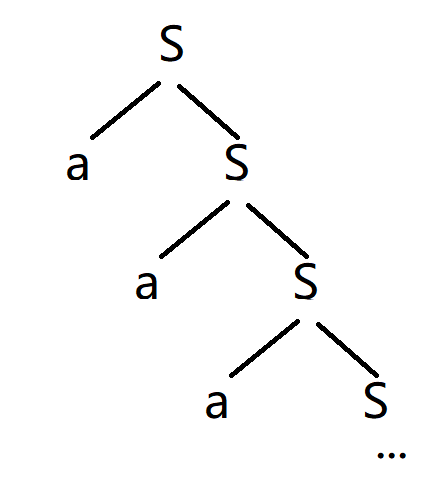
所以,前面应该都是a,语言:\(L\left( G \right) =\left\{ a^i\left( a|b \right) | i\ge 0 \right\}\)
eg2.设文法\(G_2=\left( \left\{ S \right\} ,\left\{ a, b \right\} , P, S \right)\),其中\(P\)为:(0) S->aSb (1)S->ab
画图:
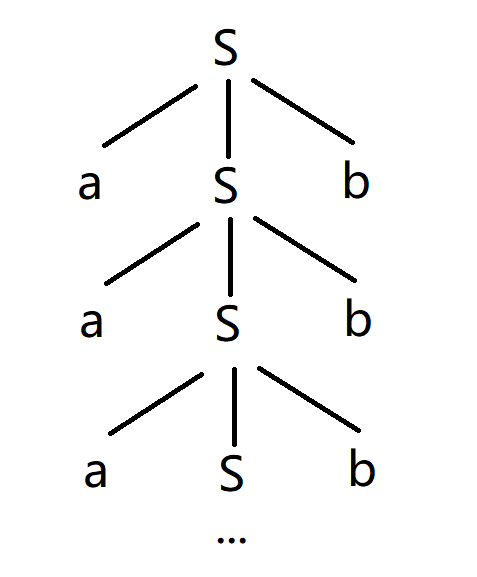
起始就是ab、aabb、aaabbb,所以文法:\(L\left( G_2 \right) =\left\{ a^nb^n| n\ge 1 \right\}\)
还有一类题目:由语言构造文法,这里还是随便举几个例子,这种题目没有什么通发,一般都是直接观察的:
例:设\(L_1=\left\{ a^{2n}b^n|n\ge 1,\text{且}a,b\in V_T \right\}\),试构造生成\(L_1\)的上下文无关文法\(G_1\)
我们先写几项出来:n = 1, L1 = aab; n = 2, L2 = aaaabb; n = 3, L3 = aaaaaabbb
观察一下,发现,每次都是在前一个的基础上增加两个a,1个b,初始状态:S->aab,后续:S->aaSb(在S的基础上,前面添加两个a,后面添加一个b,并递归)
所以最后的结果就是:S -> aaSb, S -> aab。
最后一个内容应该是语法树和二义性,这块比较简单,有空再写hhh







Comments NOTHING