首先介绍一下什么是二分图:二分图又称作二部图,是图论中的一种特殊模型,设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
官方定义有点抽象,其实就是我们可以把一个图分成两个集合,集合内部是没有变的,只有两个集合间才有边,也就是像这样的:
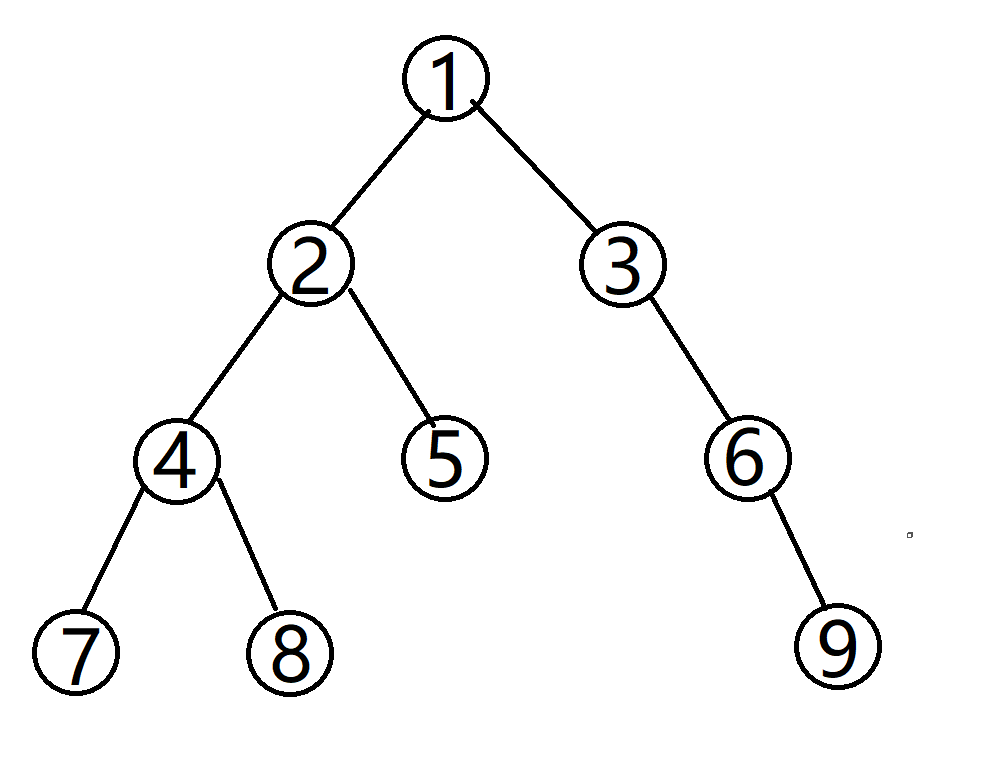
你可能看不出来,其实这是个二分图,我们变形一下:
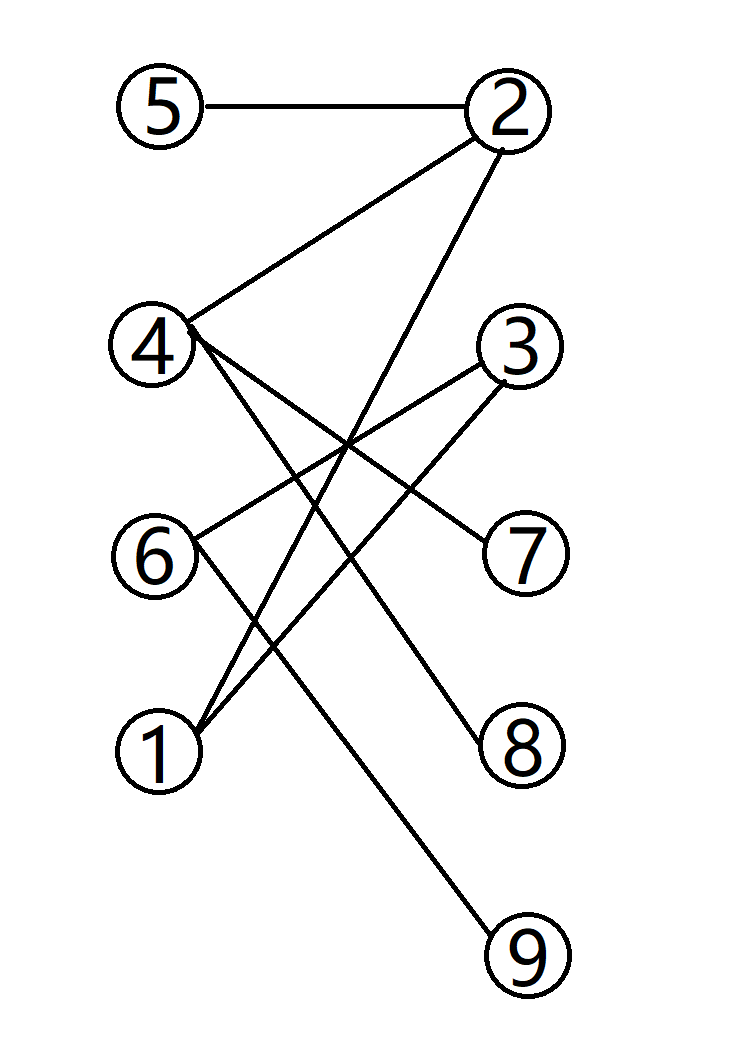
现在再看,是不是清晰多了,我们将图划分成了两个集合,集合内部是没有边的,而在集合之间存在边。
二分图的一个等价定义是:不含奇数条边的环,为什么呢?其实很简单:
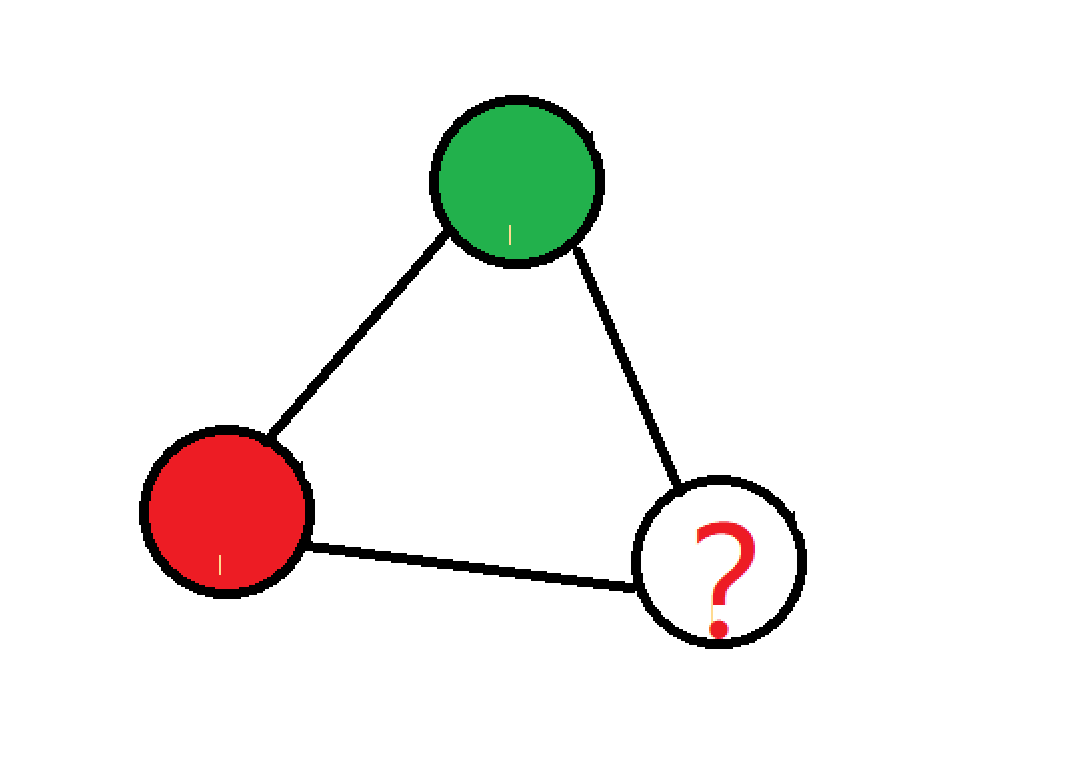
上图就是一个奇数环,我们对其染色,如果我们的这个是二分图,那我们由一条边相连的两个点的颜色应该是不同的,但是这里有了冲突,那么它就不是二分图。
这就引出了我们如何判断一个图是否为二分图:染色法
染色法判断二分图
我们对第一个例子做一个模拟:
先把第一个点染成真实一点的颜色:
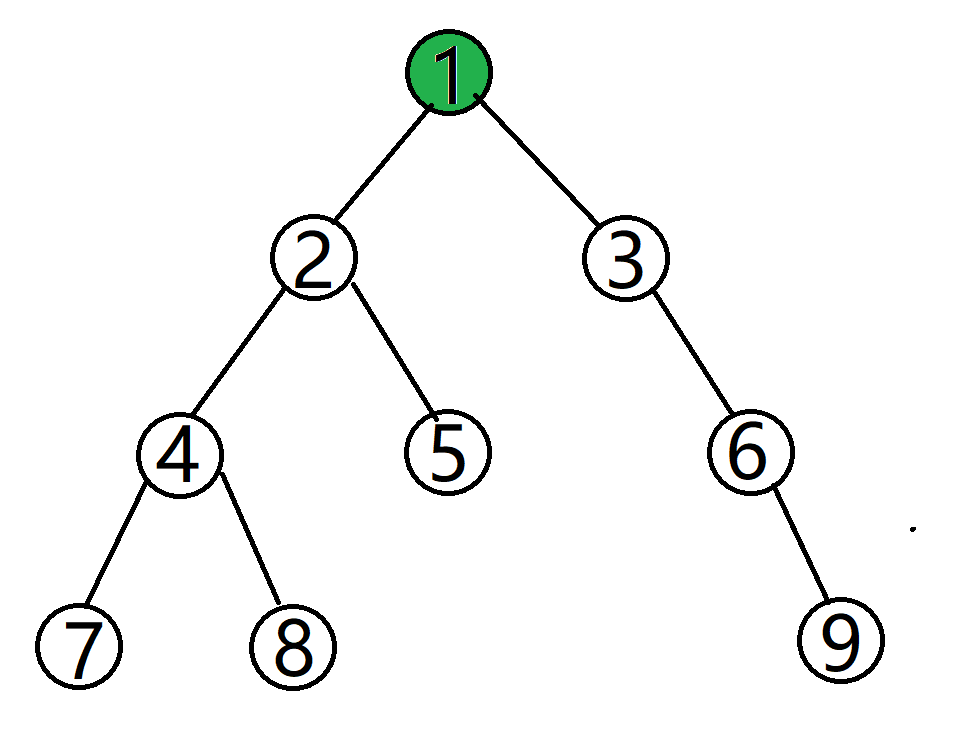
然后邻边染上不同的颜色:
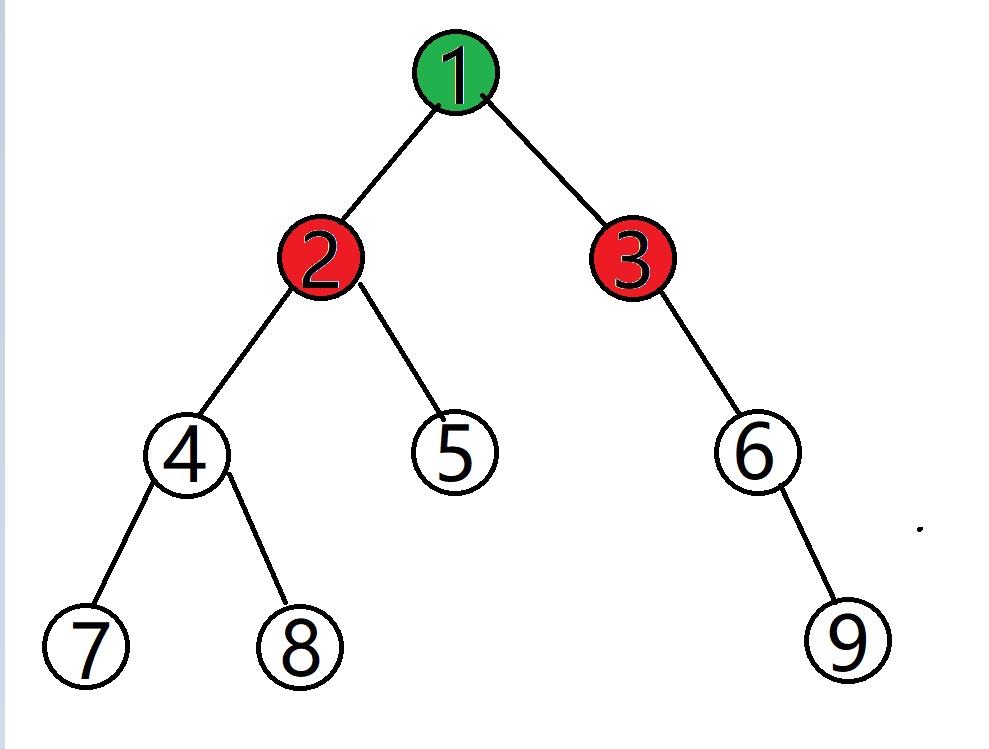
继续
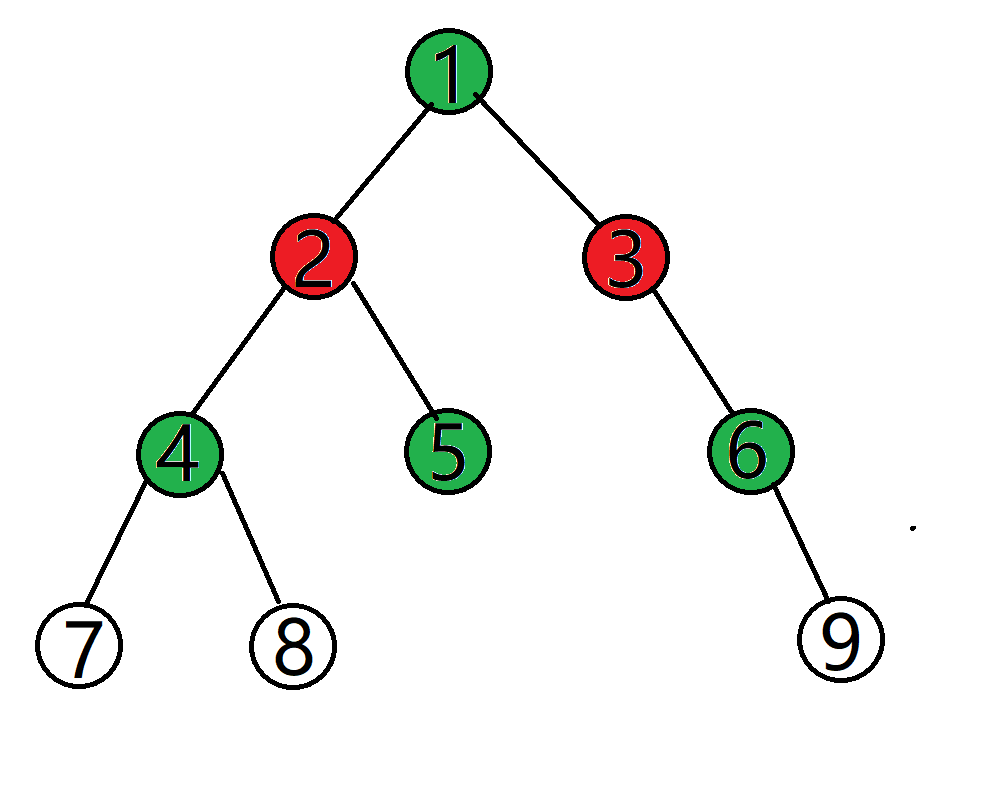
最后
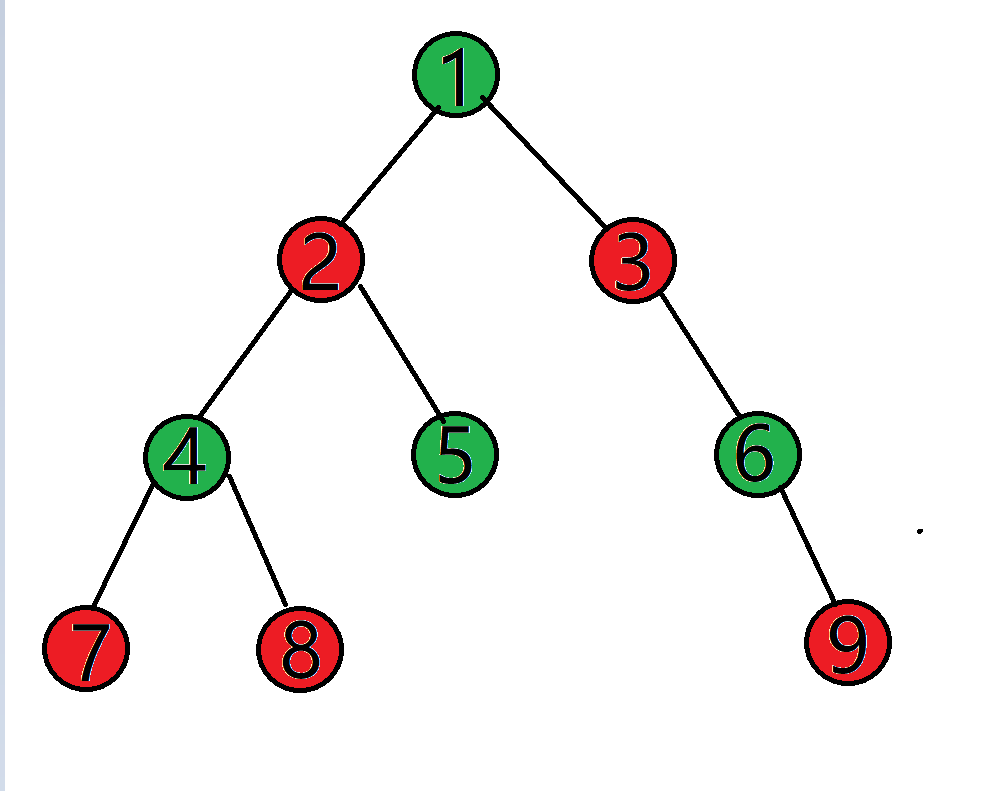
至此,我们的染色结束,在染色的过程中,我们并没有发生冲突,那就说明此图确实是二分图,如果且一旦发生冲突,那就说明这个图不是二分图,下面看一道模板题:
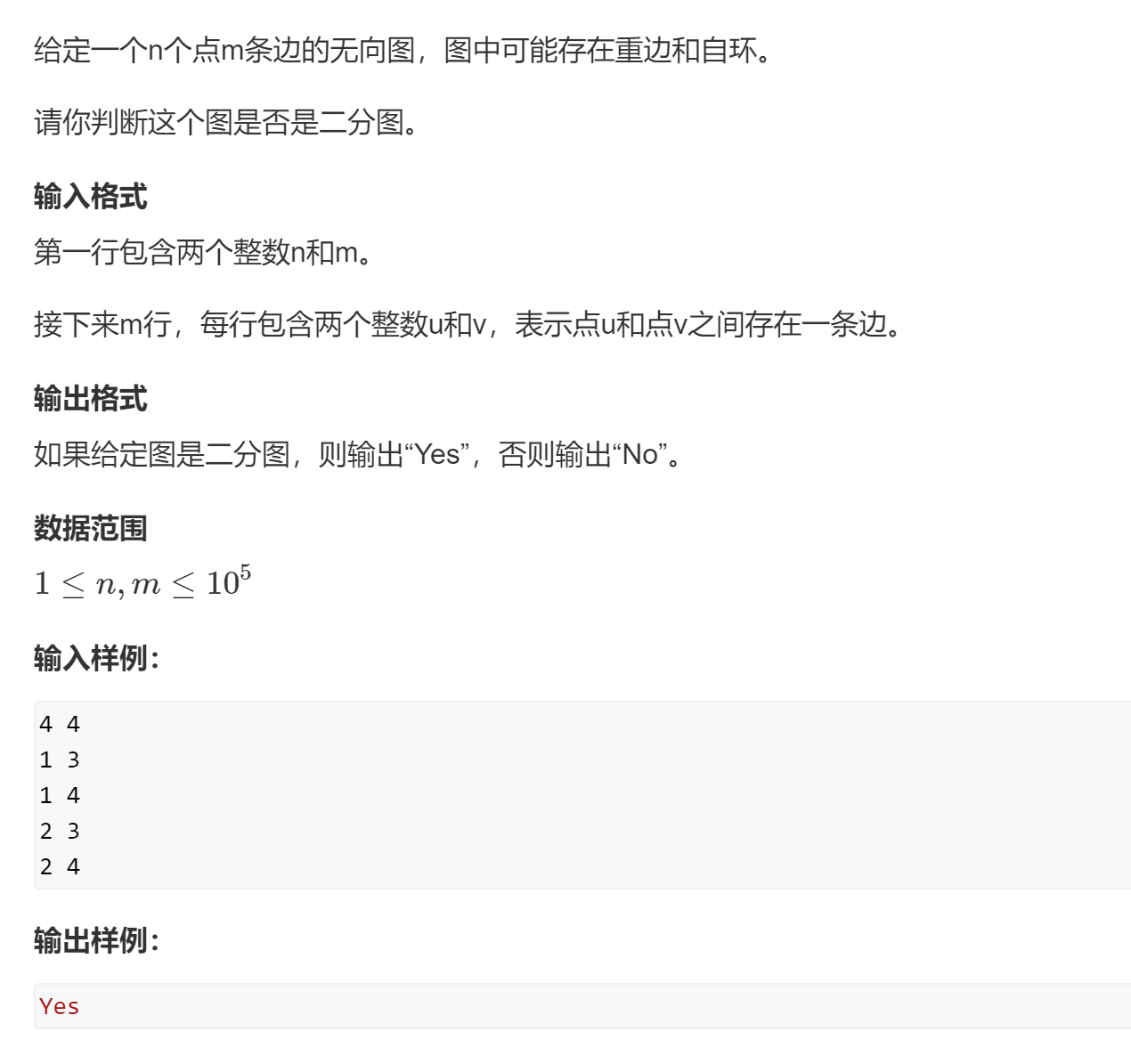
直接给出模板:
//染色法判断二分图
#include<iostream>
#include<cstring>
using namespace std;
int n, m;
const int N = 1e6;
int h[N], e[N], ne[N], idx;
int color[N];
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
bool dfs(int cur, int c) { //给当前点染上c这种颜色,并判断是否冲突,冲突返回false,否则返回true
color[cur] = c; //染色
for(int i = h[cur]; i != -1; i = ne[i]) { //枚举每条邻边
int j = e[i];
if(!color[j]) { //如果还没染色
if(!dfs(j, 3 - c)) return false; //把1变成2,把2变成1,并递归判断是否冲突
} else if(color[j] == c) { //如果染了颜色,但是已经和现有的冲突了,直接返回false
return false;
}
}
return true; //如果本次染色没有发生冲突,返回true
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
while( m -- ) {
int u, v;
cin >> u >> v;
add(u, v);
add(v, u);
}
bool flag = true;
for(int i = 1; i <= n; ++i) {
if(!color[i]) { //如果没有染过颜色
if(!dfs(i, 1)) { //把这个点染成第一种颜色
flag = false; //如果在染色过程中发生了冲突
break;
}
}
}
if(flag) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
} 二分图的最大匹配(匈牙利算法)
首先要明白匹配的概念:“任意两条边都没有公共端点” 的边的集合被称为图的一组匹配。
而所谓的最大匹配:包含边数最多的一组被称为二分图的最大匹配,二分图的最大匹配其实就是特殊的最大流问题
增广路径:该算法也被称为增广路算法,每次从左部的点找与右部匹配的点时,我们需要去找一条增广路径,如果该路径存在,说明可以将目前的所有点进行匹配,反之则右部则没有与之左部相匹配的点。
我们引入有趣的游戏来模拟一下这个过程,假设下面这张图中,左边是男生,右边是妹子(自古红蓝出CP嘛),黑色的连线代表他们之间互有好感,我们的任务就是,让尽可能多的男生和女生匹配,我们就来模拟一下匈牙利算法的过程
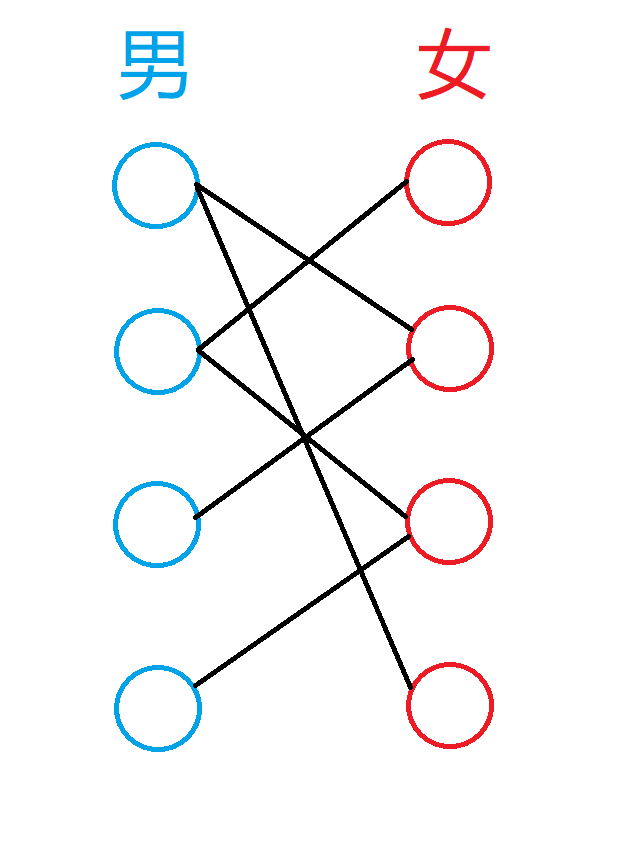
首先第一步,一号男生和三号女生有好感,撮合他们,将他们用月老的红线连起来:
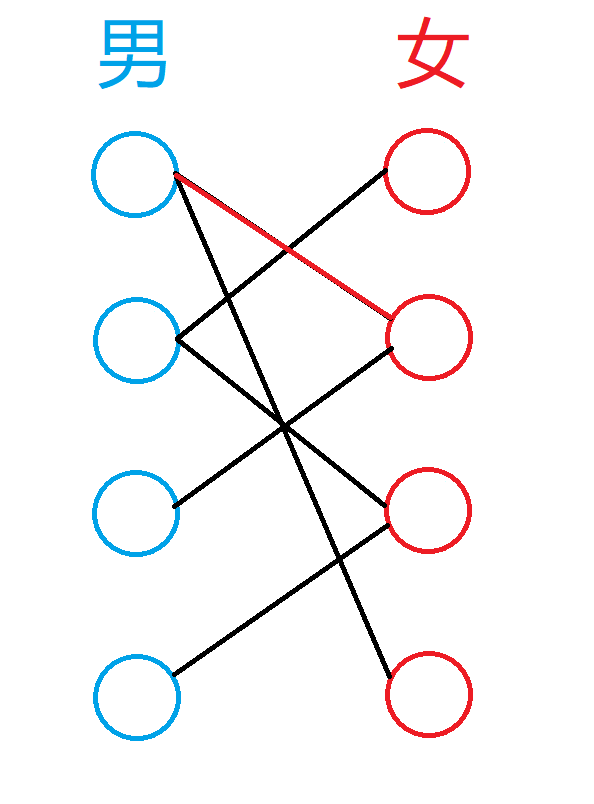
然后二号男生和一号女生有好感,将他们连起来
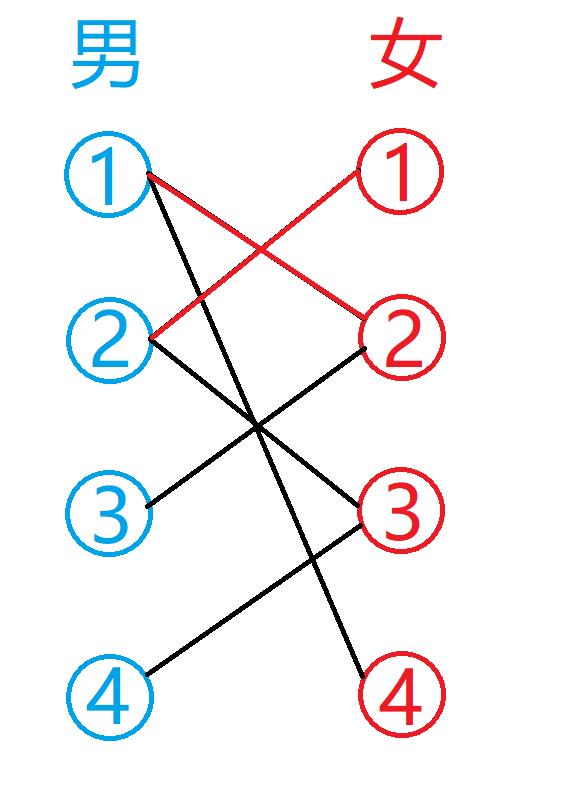
下一步,三号男生对二号女生有好感,但是问题来了,人家二号女生有对象了!!那怎么办呢?三号男生依旧不依不挠,本着坚持不退缩的勇气!他发现二号女生的对象——一号男生,居然还对四号女生有好感,啧啧,这机会不就来了吗,于是他对一号男生说,”兄弟,我觉得你和4号挺有缘的,要不你把你的女朋友让给我呗“,一号男生一听,好像有那么点道理,而且自己和二号女生相处这么久确实也腻了,于是就嘿嘿嘿。
于是经过一番骚操作之后,就变成了:一号男生把二号妹子绿了,然后和四号妹子牵手了,这时候三号男生终于实现了人生理想,和二号妹子牵手了。

下一步,四号男生对三号妹子互有好感,且三号妹子是单身,直接红线安排:

好了,红线连接的,就是二分图的最大匹配了。hhh
下面来看一道模板题,同时我给出代码板子:

代码模板:
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e6;
int h[N], ne[N], e[N], idx;
int match[N];
bool vis[N];
//vis数组用来保证本次匹配过程中,第二个集合中的每个点只被遍历一次,防止死循环。
//match存的是第二个集合中的每个点当前匹配的点是哪个,但就算某个点当前已经匹配了某个点,也有可能被再次遍历,所以不能起到判重的作用。
int ans;
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx ++ ;
}
bool find(int x) {
for(int i = h[x]; i != -1; i = ne[i]) { //遍历这个男生有好感的每个妹子
int j = e[i]; //j就是妹子的编号
if(!vis[j]) { //如果这个妹子还是单身
vis[j] = true; //通过先赋值vis[j]为true,这样在find(match[j])时,不会重复再找该女生
if(match[j] == 0 || find(match[j])) { //如果这个妹子没牵过手,或者说他现在的对象可以把她绿掉
match[j] = x; //那么就牵手成功
return true;
}
}
}
return false; //如果一次都没成功,那就失败了
}
int main() {
memset(h, -1, sizeof h);
int n1, n2, m;
cin >> n1 >> n2 >> m;
while(m -- ) {
int u, v;
cin >> u >> v;
add(u, v); //因为我们每次都是从男生开始选择女生,所以只加单向边
}
for(int i = 1; i <= n1; ++i) {
memset(vis, false, sizeof vis); //不管你有没有对象,我都要试试!
if(find(i)) { //如果帮i找到了对象,匹配数+1
ans ++ ;
}
}
cout << ans << endl;
return 0;
} 二分图的染色判定和最大匹配都是非常简单而且实用的算法,如果代码有地方看不懂的话欢迎留言哦。
结尾彩蛋:
一定要记得尝试,一定不要退缩
很多时候,让我们后悔的事并不是做错,而是错过







Comments NOTHING