我们上一篇文章介绍过多元线性回归模型,估计回归系数使用的OLS,并在最后探讨了异方差和多重共线性对模型的影响,其实回归中关于自变量的选择方法很多,变量过多时可能会导致多重共线性的问题造成回归系数不显著,甚至造成OLS估计失效,而岭回归和lasso回归在OLS回归模型的损失函数上加上了不同的惩罚项,该惩罚项由回归系数的函数构成,一方面,加入的惩罚项能够识别出模型中不重要的变量,对模型起到化简的作用,可以看作时逐步回归的升级版,另一方面,加入的惩罚项能够让模型变得可估计。
岭回归模型的原理
岭回归(Ridge regression)的原理和OLS估计类似,但是对系数的大小设置了惩罚项
多元线性回归:\(\widehat{\beta }=\underset{\widehat{\beta }}{arg\min}\sum_{i=1}^n{\left( y_i-x_{i}^{'}\widehat{\beta } \right) ^2}, \widehat{\beta }=\left( \widehat{\beta _1},\widehat{\beta _2},\cdots ,\widehat{\beta _n} \right) '\)
岭回归:

其中,\(\lambda\)为一个正的常数,同时记
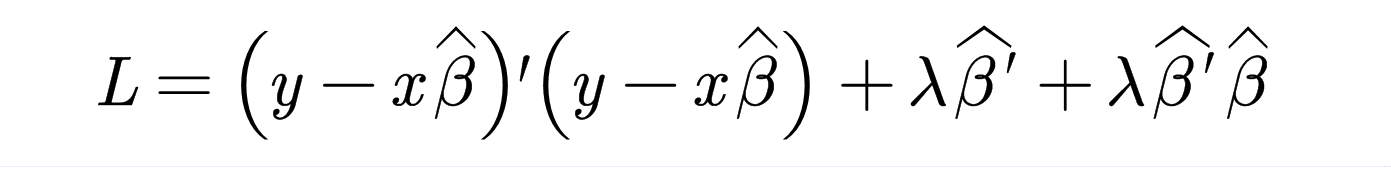
当\(\lambda \rightarrow 0\)时,岭回归和多元线性回归完全相同,当\(\lambda \rightarrow \infty\)时,\(\widehat{\beta }=0_{k\times 1}\)
另外:
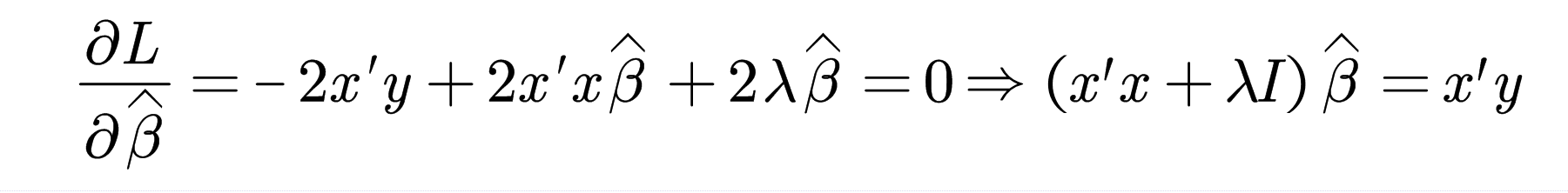
由于\(x'x\)半正定,则\(x'x\)的特征值非负,加上\(\lambda I\)后,\(x'x+\lambda I\)特征值均为正数,则\(x'x+\lambda I\)可逆,那么\(\widehat{\beta }=\left( x'x+\lambda I \right) ^{-1}x'y\left( \lambda >0 \right)\),也就是说,加入的惩罚项使得模型不会因为多重共线性的影响而估计不出来,\(\widehat{\beta }\)是一定能求出来的。
接下来的问题就是如何求\(\lambda\),一般有三种方法:
- 岭迹法
- VIF法(方差膨胀因子法)
- 最小化均方误差法
这里我就不仔细说了,因为做一个调包侠也不错,网上有很多资料,感兴趣自行搜索即可。
lasso回归的原理
lasso模型是1996年由Robert Tibshirani提出,与岭回归模型相比,其最大的优点是可以将不重要的变量的回归系数压缩至零,而岭回归虽然也对原本的系数进行了一定程度的压缩,但是任一系数都不会为零,最终的模型保留了所有的变量,所以说lasso回归可以看成是升级版的逐步回归,有点降维内味了。
lasso回归:
$$
\widehat{\beta }=\underset{\widehat{\beta }}{arg\min}\sum_{i=1}^n{\left[ \left( y_i-x_{i}^{'}\widehat{\beta } \right) ^2+\lambda \sum_{i=1}^k{|\widehat{\beta _i}|} \right]}
$$
和岭回归对比可知,lasso回归就是把平方项变成了绝对值,引入绝对值之后,等式不可以求导了,所以其无显示解,只能通过近似估计算法(坐标轴下降法和最小角回归法)
lasso回归的应用
还是使用stata来实现lasso回归:首先在电脑联网的情况下,输入命令:findit lassopack后回车
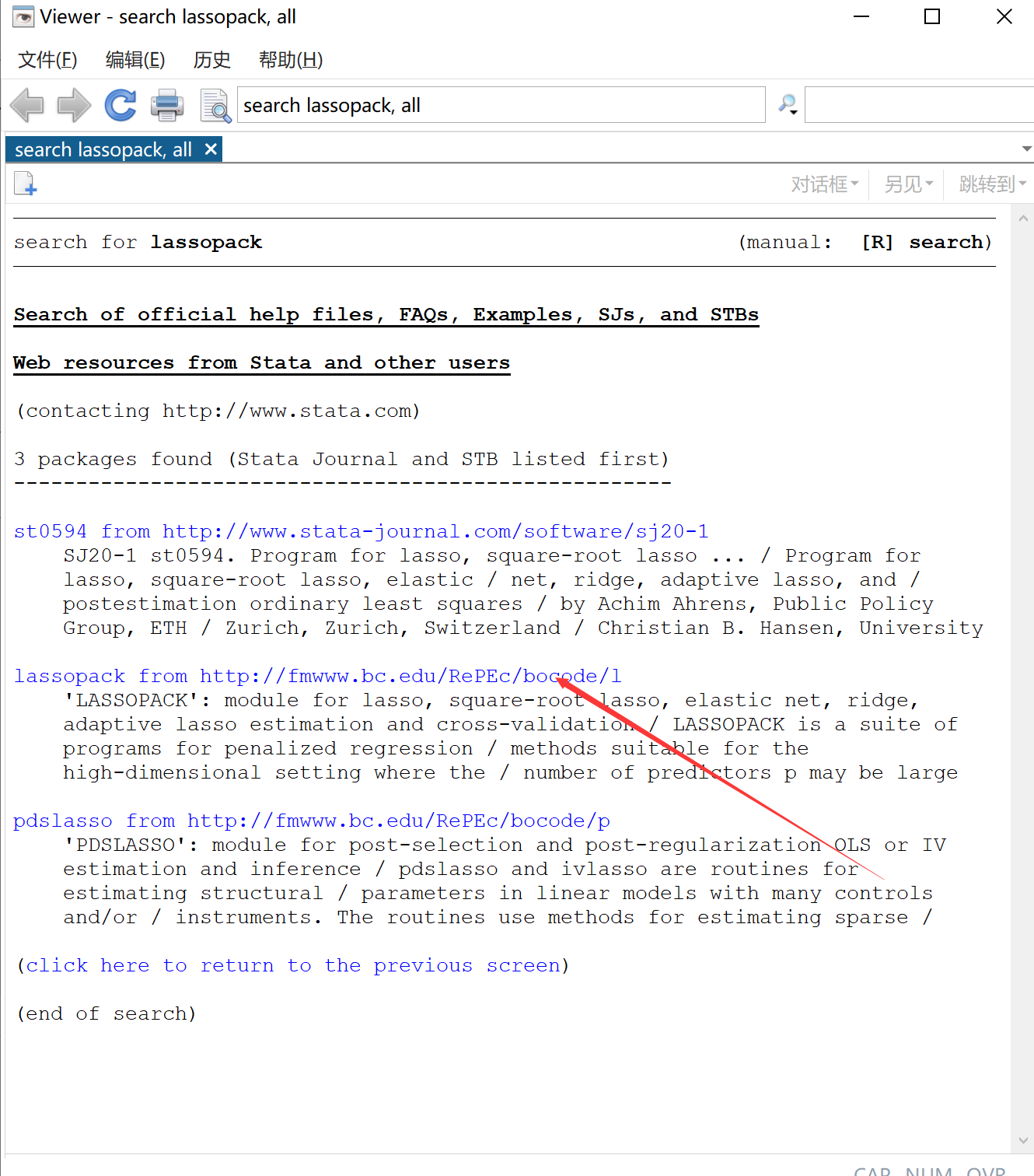
会跳出来这个页面,点击指针指向的链接,然后翻到下面,点击install
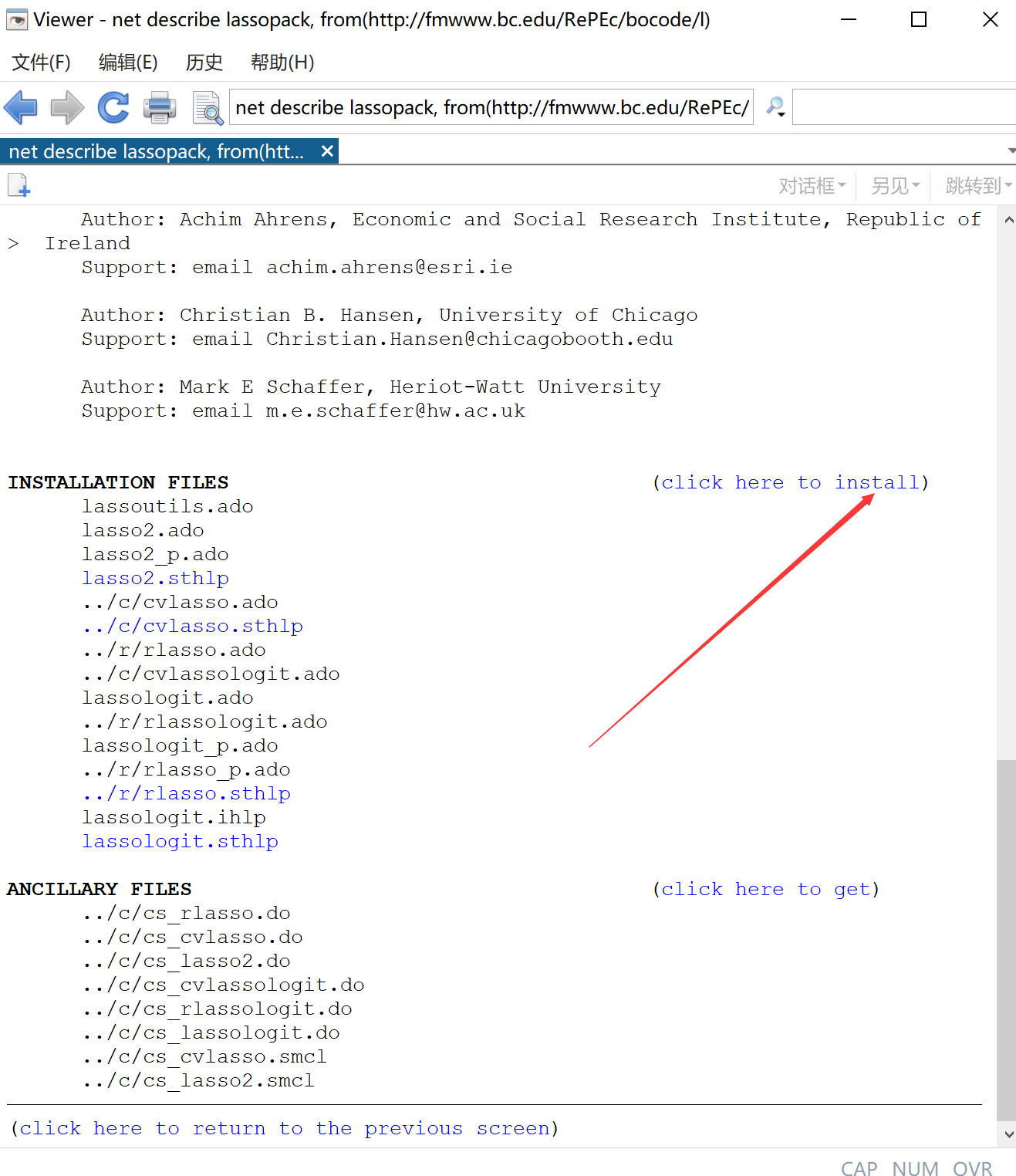
然后就可以了使用了。
还是来看一道例题,题目就用这个:http://www.vsbf.fun/?p=679
首先将excel中的数据导入到Stata中,由于量纲相同,所以这里不需要进行标准化处理,否则就需要用excel或者matlab把数据标准化一下
Stata中求\(\lambda\)采用的是K折交叉验证的方法最小化均方误差,介绍一下:
所谓的K折交叉验证,是说将样本数据随机分为K个等分。将第1 个子样本作为“验证集”(validation set)而保留不用,而使用其余K-1个子样本作为“训练集”(training set)来估计此模型,再以此预测第1 个子样本,并计算第1个子样本的“均方预测误差”(Mean Squared Prediction Error)。其次,将第2 个子样本作为验证集,而使用其余K-1 个子样本作为训练集来预测第2个子样 本,并计算第2 个子样本的MSPE。以此类推,将所有子样本的MSPE 加总, 即可得整个样本的MSPE。最后,选择调整参数,使得整个样本的MSPE 最小,故具有最佳的预测能力。
使用stata:
cvlasso 单产 种子费 化肥费 农药费 机械费 灌溉费, lopt seed(114514)稍微解释一下,这里的cvlasso就是命令,单产是因变量,后面的都是自变量,lopt表示选择使MSPE最小的\(\lambda\),选择项seed(114514)表示将随机数种子设置为114514,可以自行设定,你可以搞1919810,以便结果可重复性,默认是K=10,即:十折交叉验证
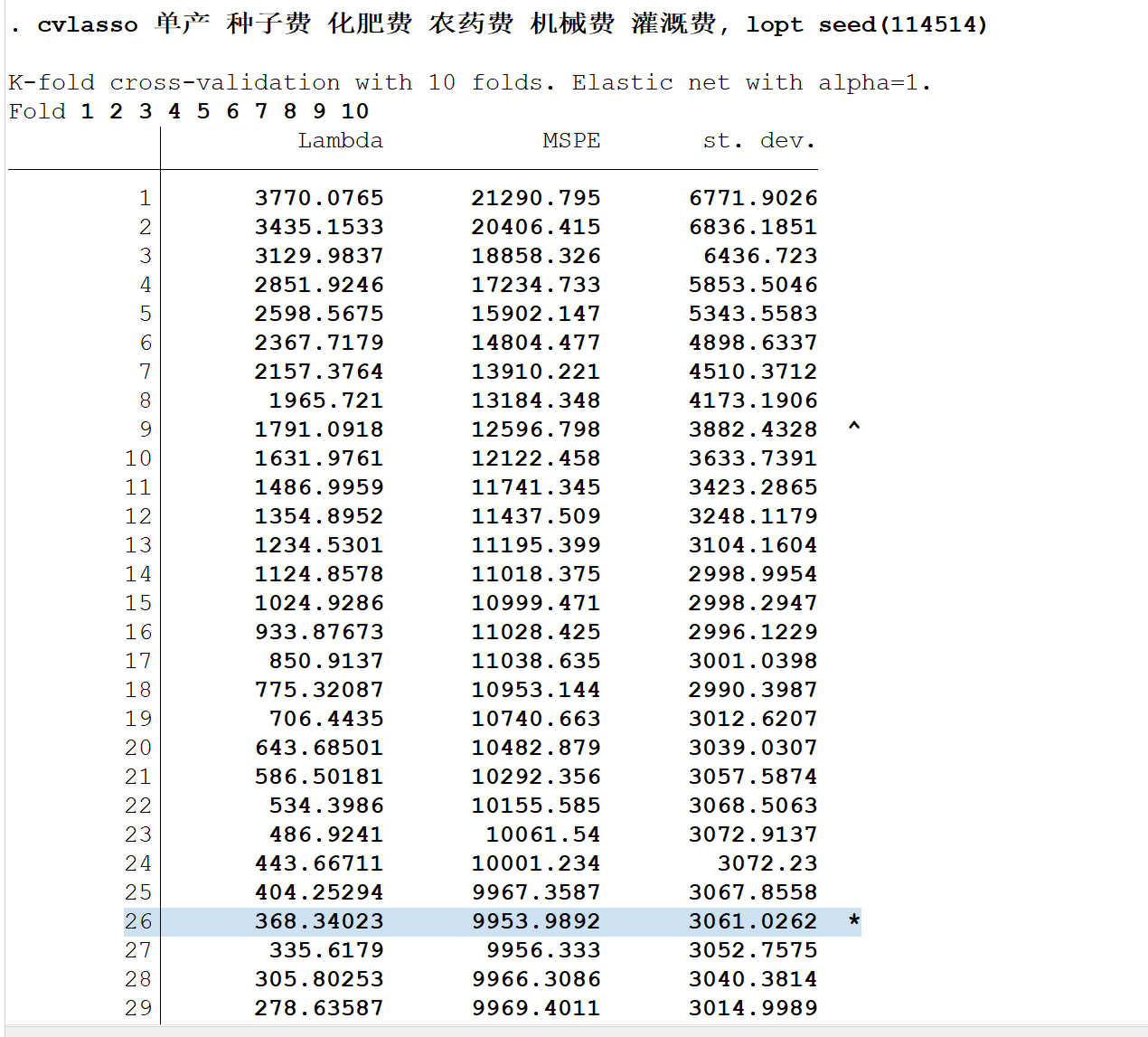
打星号的就是MSPE最小的地方,可以看出这时候的\(\lambda\)为368.34023
再来分析一下lasso给我们生成的结果:
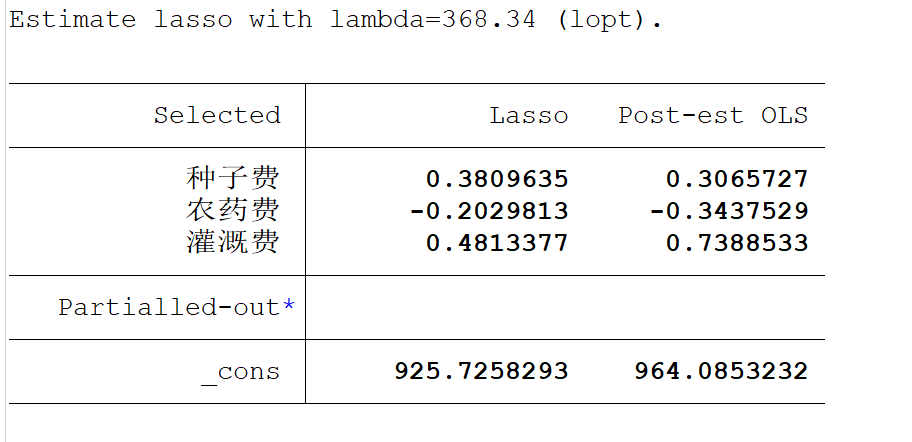
左边第一列的三个变量即为lasso所估计的变量,其他的变量都收缩至零了,所以并没有显示在上面,右边第一列`Lasso`就是lasso所估计出来的系数,'Post-est OLS'这一列指的是,仅使用lasso进行变量筛选,然后计算用的是OLS方法。
小结
何时使用lasso回归?
我们首先使用最一般的OLS对数据进行回归,然后计算方差膨胀因子VIF,如果VIF>10则说明存在多重共线性的问题,此时我们需要对变量进行筛选。这个时候,我们就可以使用lasso回归来帮我们筛选出不重要的变量,步骤如下:
(1)判断自变量的量纲是否一样,如果 不一样则首先进行标准化的预处理;(2)对变量使用lasso回归,记录下 lasso回归结果表中回归系数不为0的变量,这些变量就是最终我们要留下来的重要变量,其余未出现在表中的变量可视为引起多重共线性的不重要变量。
在得到了重要变量后,我们实际上就完成了变量筛选,此时我们只将这些重要变量视为自变量,然后进行回归,并分析回归结果即可。(注意: 此时的变量可以是标准化前的,也可以是标准化后的了,因为lasso只起到 变量筛选的目的)







Comments NOTHING