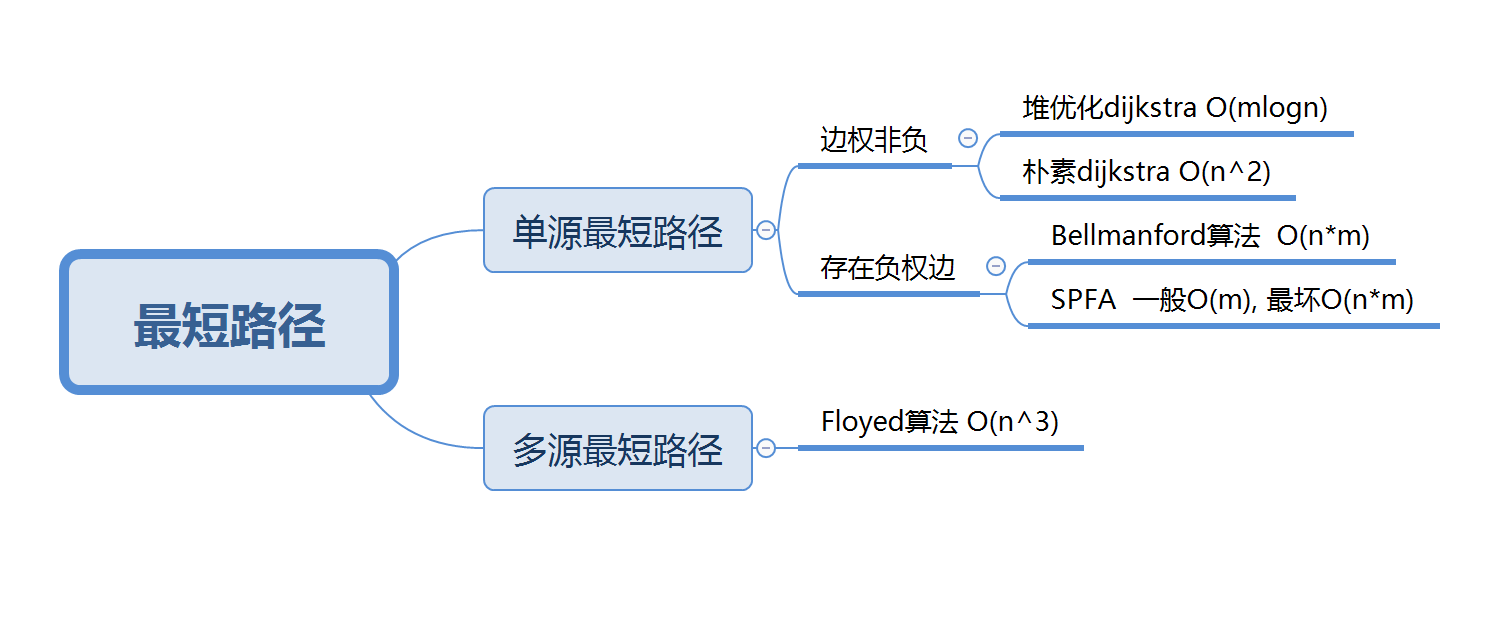
最短路径问题主要分为如下几类:
在看这篇文章之前,如果您还没有了解过最短路径问题,可以看看这个视频,现在我们来一个一个认识
单源最短路径问题
单源最短路径是指我们确定一个起点和一个终点后,我们需要求出从起点到终点的所有路径中,距离最短的一条。
朴素版Dijkstra
首先要注意:使用Dijkstra的前提条件是所有边权非负,Dijkstra算法在稠密图上的时间复杂度为\(O\left( n^2 \right)\),在稀疏图上的时间复杂度为\(O\left( m\log n \right)\)
算法思路:
- 首先初始化距离数组dist[1] = 0,也就是起点到自身的距离为零,而其他点均设置为正无穷
- 找出一个不在以选顶点集合内,且dist[x]最小的点,然后将x加入以选顶点集合
- 扫描x的所有出边,也就是所有跟节点 x 相连的边,假设y是x的出边,若dist[y] > dist[x] + z,则使用dist[y] = dist[x] + z进行更新,dist[y],这是什么意思呢,其实很简单,因为x已经固定了,如果从起点走到x加上x走到y的距离,比直接从起点走到y的距离更短,那我们就更新起点到y的距离。(这一步也被称为松弛操作)
- 重复步骤2和3,直到所有顶点都被访问
我们来看一道模板题:

在开始这道题之前我先啰嗦一下关于图的存储问题,一般存图的方式有两种,一种是直接使用邻接矩阵,另一种是使用邻接表,邻接矩阵的优势在于适合稠密图,且代码好写,邻接表适合稀疏图,代码不太好写(写多了其实也没啥...),当然邻接表也有两种写法,推荐第二种,代码更简洁,效率更高:
- 二维vector:vector<vector<int> > edge,其中edge[i][j]表示第i个点的第j条邻边
- 数组模拟(%你)邻接表,为每个点开一个单链表,分别存储该点的所有邻边。
这道题中,m的量级差不多是n的平方,也就是边数很多,属于稠密图,我们用邻接矩阵:
#include<iostream>
#include<cstring>
using namespace std;
int n, m;
const int N = 550;
int a[N][N]; //邻接表
int dist[N]; //距离数组
bool vis[N]; //已选顶点集合
int dijkstra() {
memset(dist, 0x3f, sizeof dist); //将所有点到一号点的距离都设置为正无穷
dist[1] = 0; //一号点为0
for(int i = 0; i < n; ++i) { //迭代n次
int t = -1;
for(int j = 1; j <= n; ++j) { //扫描距离信息
if(!vis[j] && (t == -1 || dist[j] < dist[t])) { //从未确定的点中找点,这个点要么是第一个点,要么是到1号点的距离比当前点的距离要近
t = j;
}
}
vis[t] = true; //加入以选顶点集合
for(int j = 1; j <= n; ++j) { //用这个点去更新别的顶点
dist[j] = min(dist[j], dist[t] + a[t][j]); //松弛操作
}
}
if(dist[n] == 0x3f3f3f3f)
return -1;
else
return dist[n];
}
int main(){
cin >> n >> m;
memset(a, 0x3f, sizeof a);
for(int i = 0; i < m; ++i) {
int x, y, z;
cin >> x >> y >> z;
a[x][y] = min(a[x][y], z); //用于处理重边
}
cout << dijkstra() << endl;
return 0;
}堆优化Dijkstra
在朴素版中,我们每次寻找到起点距离最小的顶点时,时间复杂度是\(O\left( n \right)\)的,所以我们可以使用一个小根堆来维护每个顶点到起点的距离,这样时间复杂度就可以降到\(O\left( m\log n \right)\),我们还是来看一道模板题,然后给出堆优化版的板子

由于\(n\)和\(m\)的量级相同,属于稀疏图,所以我们使用邻接表来维护
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1e6;
int h[N], w[N], e[N], ne[N], idx; //邻接表需要用到的一些数组
int n, m;
int dist[N];
bool vis[N];
typedef pair<int, int> PII;
void add(int a, int b, int c) { //建图
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx ++;
}
int dijkstra() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> que; //小根堆的定义方式
que.push({0, 1}); //表示编号为1的点距离起点的最短距离为0,因为堆是根据第一个参数来排序的,所以需要将距离放在第一个参数,将编号放在第二个参数
while(que.size()) { //只要未选顶点集合中存在元素
auto t = que.top();
que.pop();
int num = t.second, distance = t.first;
if(vis[num]) continue; //如果已经加入了已选顶点集合就不用管了
vis[num] = true; //否则加入已选顶点集合
for(int j = h[num]; j != -1; j = ne[j]) { //遍历这个点的出边
int t = e[j]; //e[j]与当前顶点的下一个点
if(dist[t] > distance + w[j]) //如果从起点到下一个顶点的距离比从起点到当前顶点的距离加上当前顶点到下一个顶点的距离的远
dist[t] = distance + w[j]; //松弛操作
que.push({dist[t], t}); 同时加入堆中,然后准备用它去更新别的点
}
}
if(dist[n] == 0x3f3f3f3f) return -1; //如果到起点的距离为无穷,说明没有路径,返回-1
else return dist[n]; //否则返回距离
}
int main(){
cin >> n >> m;
memset(h, -1, sizeof h); //首先将邻接表的头节点均设置为-1
while(m -- ) {
int x, y, z;
cin >> x >> y >> z;
add(x, y, z); //在节点与节点之间建立边
}
cout << dijkstra() << endl;
return 0;
}可以看出朴素版和堆优化版本各有优势,也不能说堆优化就一定比朴素版要好,因为如果当\(m~n^2\)时,堆优化的时间复杂度为\(O\left( n^2\log n \right)\),比朴素版要差。
Bellmanford算法
我们知道,Dijkstra唯一的缺点是不能处理负权边,所以Bellmanford算法就是来解决这个问题的,同时,bellmanford算法还有一些优势,比如实现简单,可以限定边数,缺点是时间复杂度高,但可以对其进行一些优化,提高效率。
下面的场景可以用Bellmanford算法:
- 从起点出发是否存在到达各个顶点的路径(如果计算出来了值那就可以到)
- 从起点出发到达各个顶点的最短路径
- 图中是否有负权回路
算法思路:
- 首先初始化距离数组dist[1] = 0,也就是起点到自身的距离为零,而其他点均设置为正无穷
- 后续进行n-1次遍历操作,对所有的边进行松弛操作
思路上与Dijkstra最大的不同是每次都是从源点s重新出发进行松弛操作,而Dijkstra则是从源点出发向外扩逐个处理相邻的节点,不会去重复处理节点,可以看出Dijkstra效率相对更高点。
下面来看一道模板题:

题目大意是说让我们求1号点到n号点的最多经过k条边的最短距离
#include<iostream>
#include<cstring>
using namespace std;
const int N = 550;
const int M = 100010;
int dist[N], backup[N];
int n, m, k;
struct vertex{ //因为我们每次松弛时,需要遍历每条边,所以不用建图,直接用结构体存起来就行
int a, b, w;
} edges[M];
int bellmanford() {
memset(dist, 0x3f, sizeof dist); //初始化
dist[1] = 0;
for(int i = 0; i < k; ++i) { //因为有边数限制,所以松弛k次
memcpy(backup, dist, sizeof dist); //backup数组是上一次迭代后dist数组的备份,由于是每个点同时向外出发,因此需要对dist数组进行备份,若不进行备份会因此发生串联效应,影响到下一个点
for(int j = 0; j < m; ++j) { //对于每条边
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], backup[a] + w); //这里在松弛时要注意使用上一次迭代后的值来更新
}
}
if(dist[n] > 0x3f3f3f3f/2) return -1; //因为我们在路径上可能会存在负的边权,而我们的距离初始化为0x3f3f3f3f,所以在遍历的过程中,可能会加上一些负的权值导致0x3f3f3f3f会变小一点,所以用判断是否大于除以2后的值来决定是否返回-1
return dist[n];
}
int main() {
cin >> n >> m >> k;
for(int i = 0; i < m; ++i) {
int a, b, c;
cin >> a >> b >> c;
edges[i] = {a, b, c};
}
int t = bellmanford();
if(t == -1) cout << "impossible" << endl;
else cout << t << endl;
return 0;
}SPFA
可以看出bellmanford虽然应用范围广,但并不优秀(指时间复杂度),而SPFA算法就是bellmanford的队列优化。
算法思路:使用dist数组记录每个节点的最短路径值,首先定义一个队列来保存需要优化的顶点,优化时每次取出首节点,并使用首节点对其所有 有联系的顶点v进行松弛操作,如果v点不在当前的队列中,就将v放进队尾,不断取出节点进行松弛操作,直到队列为空,所以时间复杂度最好为\(O\left( m \right)\),最坏为\(O\left( m*n \right)\)。
可以看出,其思路和bfs基本相同,代码和bfs也基本一样,我们还是来看一道模板题感受一下。

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
int n, m;
const int N = 1e6 + 10;
int h[N], w[N], e[N], ne[N], idx; //还是使用邻接表来存图
int dist[N];
bool vis[N];
void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx ++;
}
int spfa() {
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> que;
que.push(1); //1号节点进队,准备把他处理
vis[1] = true;
while(que.size()) {
int t = que.front(); //出队
que.pop();
vis[t] = false;
for(int i = h[t]; i != -1; i = ne[i]) { //扩展
int j = e[i];
if(dist[j] > dist[t] + w[i]) { //松弛
dist[j] = dist[t] + w[i];
if(!vis[j]) { //入队
que.push(j);
vis[j] = true;
}
}
}
}
return dist[n];
}
int main(){
memset(h, -1, sizeof h);
cin >> n >> m;
while(m -- ) {
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
}
int t = spfa();
if(t == 0x3f3f3f3f) cout << "impossible" << endl;
else cout << t << endl;
return 0;
}经常有人说在算法竞赛中SPFA已死,其实我觉得,如果题目中有负权边,dijkstra无能为力的时候,也就只能bellmanford算法和SPFA了,但是SPFA在最坏情况下也与bellmanford时间复杂度相同,貌似bellmanford好像没啥存在的必要(欢迎反驳),我查过卡SPFA的情况,也就是当给定的图为“菊花图”或者“网格图”时,每次都有一大批小萌新入队准备接受调教,这个时候就会很慢。如果是随机图,SPFA一般也比Dijkstra跑的要快。
反正能用DIjkstra就用Dijkstra,如果存在负权图,直接SPFA就好了。
多源最短路径
多源最短路径就只有Floyed算法一个,Floyed是基于动态规划的思想设计的,而Dijkstra是基于贪心的思想。
Floyed的思想非常好理解,从任意顶点\(i\)到任意顶点\(j\),一般就两种情况,一种是从\(i\)直接到\(j\),另一种是从\(i\)经过若干个节点\(k\)到\(j\),我们在这两种情况中取min就好了。
还是一道模板题:

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n, m, k;
const int N = 251; //别问我为啥是251,问就是充满智慧
int graph[N][N];
void floyd() { //核心代码,就四行
for(int k = 1; k <= n; ++k) {
for(int i = 1; i <= n; ++i) {
for(int j = 1; j <= n; ++j) {
graph[i][j] = min(graph[i][j] , graph[i][k] + graph[k][j]);
}
}
}
}
int main() {
cin >> n >> m >> k;
for(int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if(i == j) graph[i][j] = 0; //自己到自己肯定是0
else graph[i][j] = 1e9; //到其他点初始化为无穷
}
}
while(m--) {
int x, y, z;
cin >> x >> y >> z;
graph[x][y] = min(graph[x][y], z); //如果有重边,就取最小的
}
floyd();
while(k -- ) {
int a, b;
cin >> a >> b;
if(graph[a][b] > 1e9 / 2) //这个地方和bellmanford一样,会经过负权边
cout << "impossible" << endl;
else
cout << graph[a][b] << endl;
}
return 0;
}







Comments NOTHING