P2249 查找
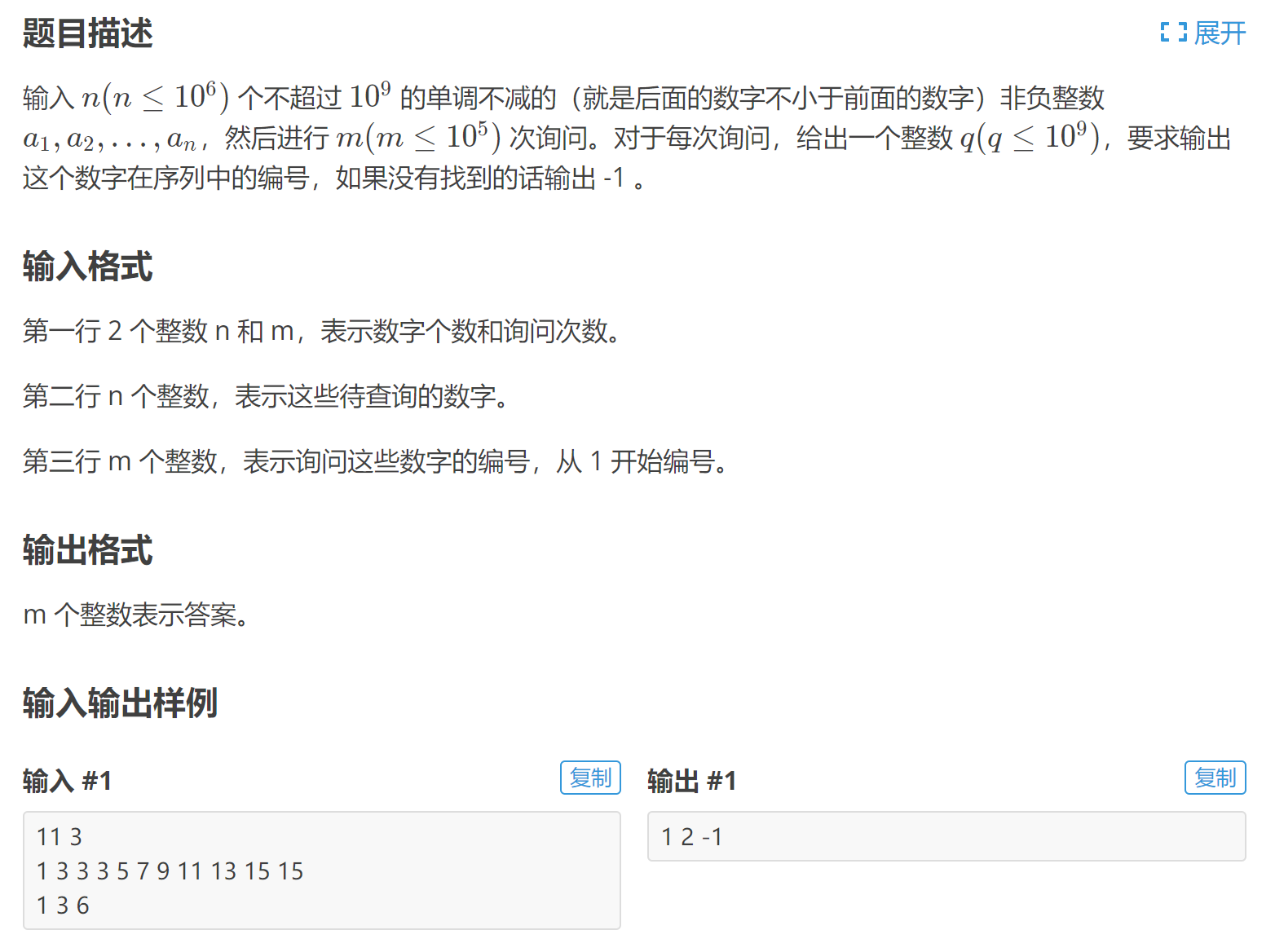
在数组中查找点,可以直接使用模板一,也可以使用模板二
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N];
int n, m;
int find(int k) {
int l = 0, r = n - 1;
int mid;
while(l < r) {
mid = l + r >> 1;
if(a[mid] >= k) { //查找大于等于k的第一个元素,其实就是k本身
r = mid;
} else {
l = mid + 1;
}
}
if(a[r] == k) { //如果最终的结果查找正确,返回r+1,因为数组下标是从零开始的,而题目要求从1编号
return r + 1;
} else {
return -1;
}
}
int main(){
cin >> n >> m;
for(int i = 0; i < n; ++i) {
cin >> a[i];
}
while(m --) {
int k;
cin >> k;
cout << find(k) << " ";
}
return 0;
}
P1102 A-B 数对

\(A-B = C\)不好求,我们可以转化成\(A=B+C\),《挑战程序设计竞赛》上讲过这个黑科技。
所以我们可以使用一个循环枚举\(B\),如果数组有序,那么在\(B\)的后方会存在一个数满足\(A-B=C\),所以我们只需要找出从当前位置到\(n\)中,小于等于\(B+C\)和小于\(B+C\)的位置,然后再将其相减就得到了数对的个数,每次循环我们都需要将这个差值累计起来,最终这个累计值就是答案了。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 2e5 + 10;
int a[N];
long long ans = 0;
int find_left(int l, int r, int k) {
while(l < r) {
int mid = l + r + 1 >> 1;
if(a[mid] < k) { //寻找小于k的最后一个元素
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
int find_right(int l, int r, int k) {
while(l < r) {
int mid = l + r + 1 >> 1;
if(a[mid] <= k) { //寻找小于等于k的最后一个元素
l = mid;
} else {
r = mid - 1;
}
}
return l;
}
int main(){
int n, c;
cin >> n >> c;
for(int i = 1; i <= n; ++i) {
cin >> a[i];
}
sort(a + 1, a + 1 + n); //必须要先排序
for(int i = 1; i <= n; ++i) {
int l = find_left(i, n , a[i] + c); //从i到n查找a[i] + c
int r = find_right(i, n, a[i] + c);
cout << l << " " << r << endl;
ans += r - l; //如果不存在的话,r - l就是零
}
cout << ans;
return 0;
}
P1873 砍树
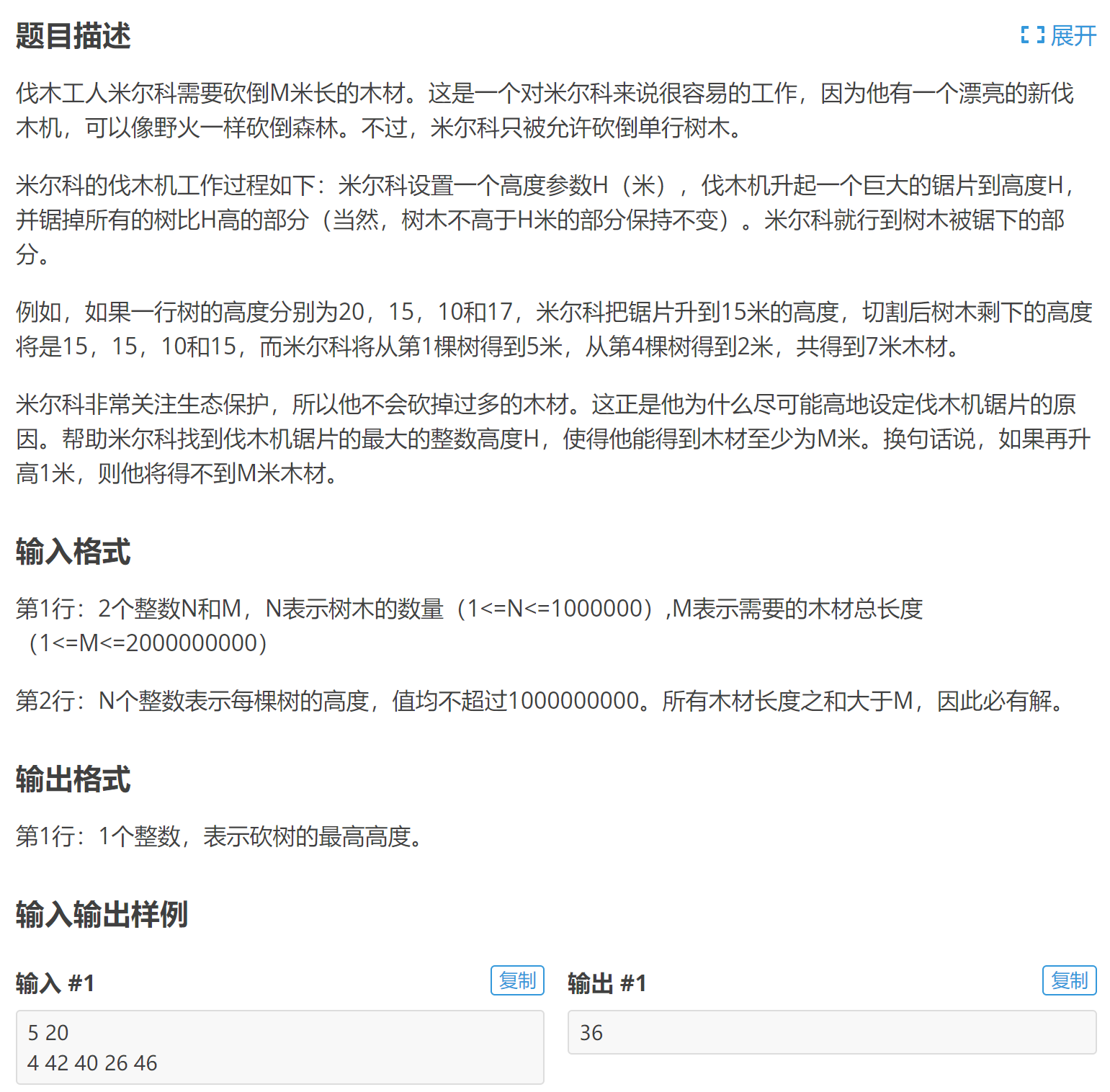
题目中有一句话“如果再升高1米,则他将得不到M米木材”,其实这个地方就暗示我们答案是满足最大化最小(小于M的最大值)这一条性质,那么就直接二分答案,二分边界l=0, r=max(树的高度),每次枚举一个\(H\),看是否满足题意:
#include<iostream>
using namespace std;
const int N = 1000005;
long long a[N];
long long m, n;
long long check(int H) {
long long sum = 0;
for(int i = 0; i < n; ++i) {
if(a[i] > H) //如果可以砍
sum += a[i] - H; //将获得的木材累计起来
}
return sum;
}
int main(){
cin >> n >> m;
int _max = -1;
for(long long i = 0; i < n; ++i) {
cin >> a[i];
if(a[i] > _max) _max = a[i];
}
long long l = 0, r = _max;
while(l < r) {
long long mid = l + r >> 1;
if(check(mid) < m) { //如果木材少了
r = mid; //减少H,增加木材
} else {
l = mid + 1;
}
}
cout << r - 1 << endl;
return 0;
}
P1024 一元三次方程求解

其实博主最早接触的二分应该就是这个例子,貌似是高一数学里面的内容,大家应该也都学过,但是后面用的很少(基本不用)。
因为根与根之间的绝对值大于等于1,所以说我们可以每次二分一个区间,这个区间的端点就是两个相邻的整数,而答案就是:要么在区间端点,这个我们可以提前特判一下,要么在区间内部,此时\(f(l)\times(r) < 0\)
#include<iostream>
#include<vector>
#include<algorithm>
#include<cstdio>
using namespace std;
double a, b, c, d;
double f(double x) {
return a * x * x * x + b * x * x + c * x + d;
}
vector<double> ans;
int main(){
cin >> a >> b >> c >> d;
for(int i = -100; i <= 100; ++i) {
double l = i, r = i + 1; //每次枚举一个区间
if(f(l) == 0) {
ans.push_back(l);
}
if(f(l) * f(r) < 0) { //如果发现两根之积为负数,则说明这个区间有根
while(r - l >= 0.000001) { //实数二分随便写
double mid = (l + r) / 2;
if(f(l) * f(mid) <= 0) {
r = mid;
} else {
l = mid;
}
}
ans.push_back(l);
}
if(ans.size() == 3) break;
}
sort(ans.begin(), ans.end());
printf("%.2lf %.2lf %.2lf", ans[0], ans[1], ans[2]);
return 0;
}
P1678 烦恼的高考志愿
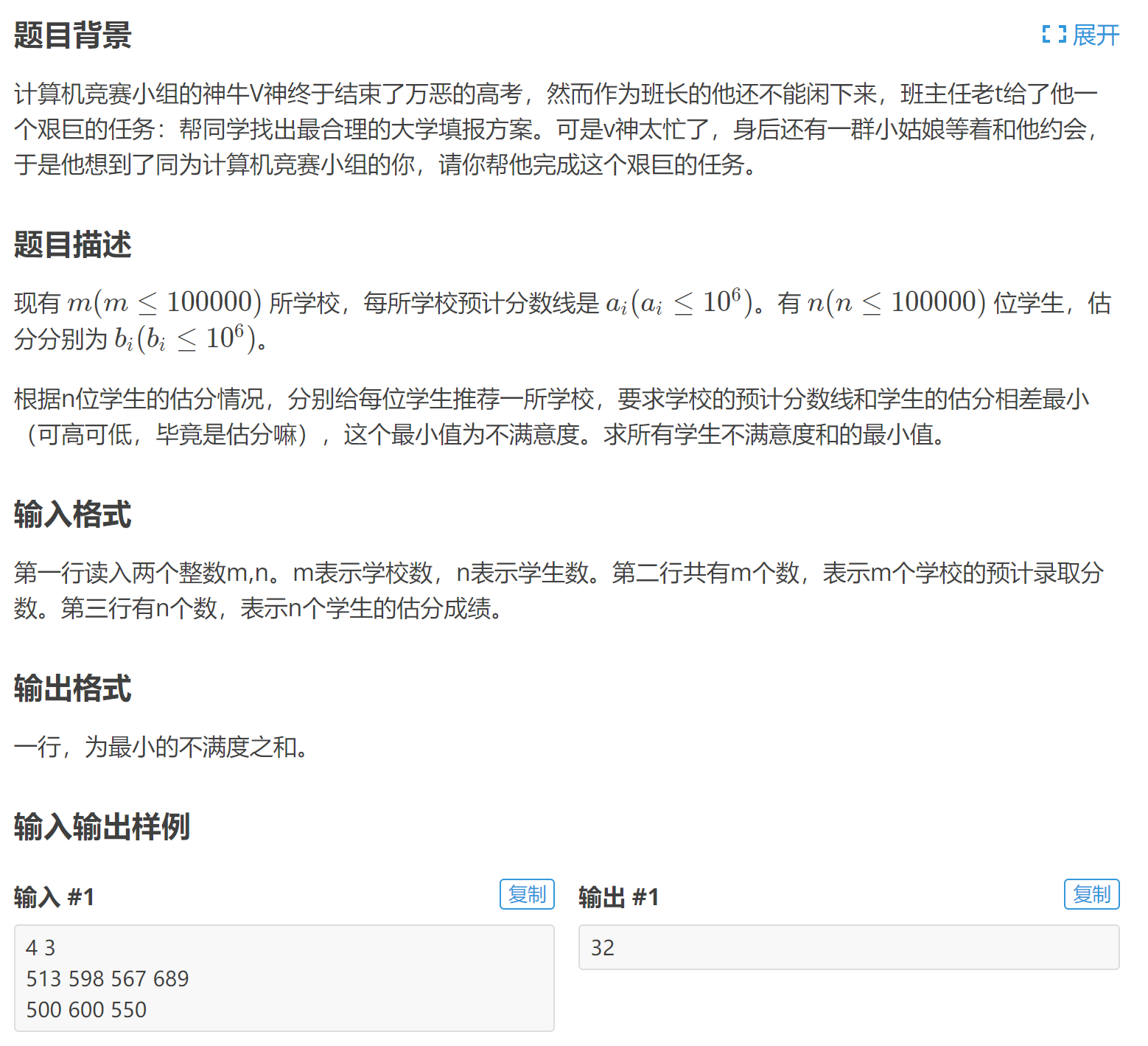
首先对每所大学的分数线排序,然后对于每个学生,查找刚好比他分数线高一点的大学,然后在前一个大学和这个分数线高一点的大学中选择最优的,思路非常简单,直接看代码就能看懂了。
#include<iostream>
#include<cmath>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 1e6 + 10;
vector<int> a;
int b[N];
int n, m;
int find(int k) {
int l = 0, r = m - 1;
while(l < r) {
int mid = l + r >> 1;
if(a[mid] >= k) { //寻找大于等于k的第一个元素
r = mid;
} else {
l = mid + 1;
}
}
return r;
}
int main(){
cin >> m >> n;
for(int i = 0; i < m; ++i) {
int k; cin >> k;
a.push_back(k);
}
for(int i = 0; i < n; ++i) {
cin >> b[i];
}
int ans = 0;
sort(a.begin(), a.end());
for(int i = 0; i < n; ++i) {
int k = find(b[i]);
if(b[i] <= a[0]) { //如果是在最左边
ans += a[0] - b[i]; //直接是第一个
} else {
ans += min(abs(a[k - 1] - b[i]), abs(a[k] - b[i])); //在前一个和后一个中选择最优的
}
}
cout << ans << endl;
return 0;
}
P2440 木材加工
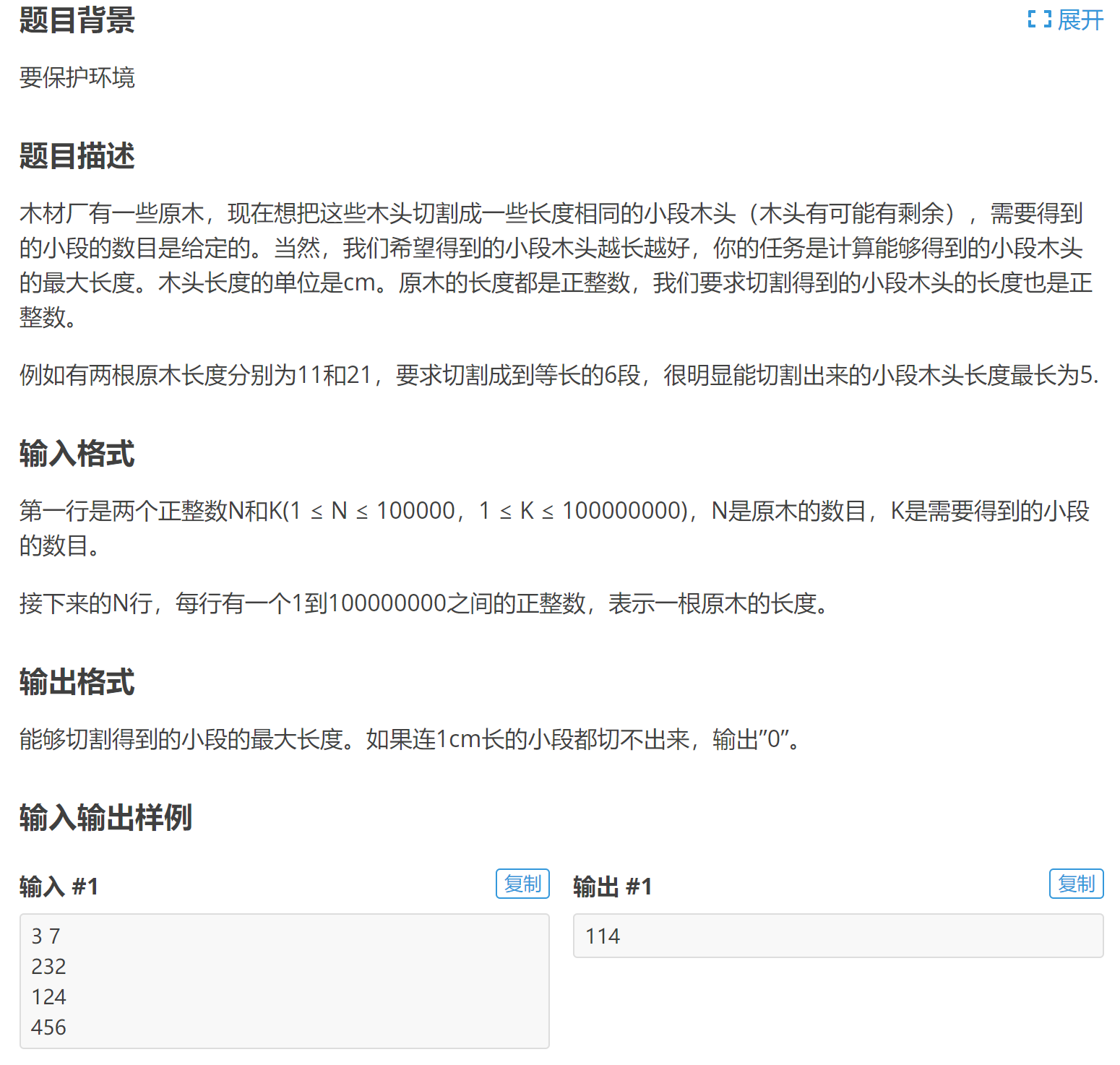
我们直接二分答案,答案的最小值当然就是零,答案的最大值也就是题目告诉我们的“每行有一个1到100000000”之间的正整数,那我们就直接设置\(r=max+1\)就好了,然后我们搜索每个长度,当然是二分搜索了,然后看能不能符合题目中要获得的小段数目就好了。注意这里要求的是满足答案的最大值,所以我们用第三套模板。
#include<iostream>
using namespace std;
const int N = 100005;
long long a[N];
int n; long long k;
int check(int len) {
long long cnt = 0;
for(int i = 0; i < n; ++i) {
cnt += a[i] / len; //看能切多少段
}
return cnt;
}
int main(){
cin >> n >> k; long long sum = 0;
for(int i = 0; i < n; ++i) {
cin >> a[i];
}
long long l = 0, r = 100000001;
while(l < r) {
int mid = l + r + 1 >> 1;
if(check(mid) >= k) { //如果段数多了
l = mid; //增大长度,让段数变少
} else {
r = mid - 1; //否则减小长度,让段数变多
}
}
cout << l << endl; //到最后肯定是l==r退出循环,所以也可以输出r
return 0;
}
P2678 跳石头

这题当然也是直接二分答案了,最少是零,最大是L,然后我们枚举答案,看在当前答案下,最多可以移走多少块石头,然后和题目中给定的移走石头数目比较。这里也是求最小的最大,所以用第三套模板
#include<iostream>
using namespace std;
long long L, N, M;
const int n = 50005;
long long a[n];
long long check(long long k) { //跳跃距离为k时,要移走多少块石头
long long now = 0, ans = 0;
for(int i = 0; i < N; ++i) {
if(a[i] - now < k) { //如果能移,就移走
ans++;
} else {
now = a[i]; //否则我们就跳过去,更新now就好了
}
}
return ans;
}
int main(){
cin >> L >> N >> M;
for(int i = 0; i < N; ++i) {
cin >> a[i];
}
long long int l = 0, r = L;
while(l < r) {
long long mid = l + r + 1 >> 1;
if(check(mid) <= M) { //如果当前跳跃距离下移走的石头小于组委会最多可以移走的石头
l = mid; //那就说明可以跳更远一点,这样的话可以移走更多石头
} else {
r = mid - 1; //这个解行不通,得少跳一点
}
}
cout << l << endl;
return 0;
}
P3853 [TJOI2007]路标设置

我们二分搜索答案,假设空旷指数最少是零,最多是L,在当前的空旷指数下,看我们还需要增设多少个路标,如果增设的路标小于“最多可增设的路标数量”,则说明我们需要减少空旷指数,这样才能不浪费路标嘛。具体的细节看代码:
#include<iostream>
using namespace std;
const int n = 100005;
int a[n];
int check(long long K) { //空旷指数为k时,要增加路标的个数
int ans = 0;
for(int i = 0; i <= n; ++i) {
if(a[i + 1] - a[i] > K) { //如果两个路标之间的空旷指数大于了K,那就不行了啊,得插路标了
ans += (a[i + 1] - a[i]) / K; //路标的个数就是后面的距离减去前面的距离然后除以K
if((a[i + 1] - a[i]) % K == 0) //如果刚好是倍数,那么会和一个端点重合,要减去1
ans--;
}
}
return ans;
}
int main() {
long long L, N ,K;
cin >> L >> N >> K;
for(int i = 1; i <= N; ++i) {
cin >> a[i];
}
a[0] = 0, a[N + 1] = L; //两端默认的路标可别忘了
long long l = 0, r = L;
//增设的路标越多,空旷指数越小
while(l < r) {
long long mid = l + r >> 1;
if(check(mid) <= K) { //当空旷指数为mid时,需要增设的路标个数
r = mid;
} else {
l = mid + 1;
}
}
cout << l << endl;
return 0;
}
P1182 数列分段 Section II


搜索答案,对于每个答案,看看能不能分出M段,如果少于M段,那就需要我们将答案调大,减小段和值,增加段数;如果段数多了,那我们就需要将答案增大,增大段和值,减少段数。具体的细节看代码
#include<iostream>
using namespace std;
const int N = 1e5 + 5;
long long a[N];
int n, m;
int check(int k) {
int sum = 0, cnt = 0;
for(int i = 0; i < n; ++i) {
if(sum + a[i] <= k) //如果这个加上这个数,段的和的值还小于k
sum += a[i]; //那就把他加上
else {
sum = a[i]; //否则用这个数重新将sum更新,然后重新分段
cnt++;
}
}
return cnt;
}
int main(){
cin >> n >> m;
long long sum = 0;
long long _max = 0;
for(int i = 0; i < n; ++i) {
cin >> a[i];
if(a[i] > _max) _max = a[i]; //找最大值作为区间的左端点,因为无论如何l也不可能小于一个数的最大值
sum += a[i]; //找最大值
}
long long l = _max, r = sum;
while(l < r) {
int mid = l + r >> 1;
if(check(mid) < m) { //如果段数小了,那么减小段和值,增加段数
r = mid;
} else {
l = mid + 1;
}
}
cout << l << endl;
return 0;
}
P1163 银行贷款
其实这个题是有公式的,如果知道了公式,那就简单多了,由于我们这里的重点在于写二分,而不是去研究什么利率之类的东西,我们直接根据公式用实数二分来逼近就行了。
$$
\sum_{i=1}^k{\frac{m}{\left( 1+p \right) ^i}}=n\,\,\Rightarrow \sum_{i=1}^k{\frac{1}{\left( 1+p \right) ^i}}=\frac{n}{m}
$$
这个题还有一个坑就是利率不一定在100%以内...真是黑心银行
实数二分就随便写了,不用考虑什么边界条件
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
int n, m, k;
double check(double p) {
double sum = 0;
for(int i = 1; i <= k; ++i) {
sum += 1.0/pow(1 + p, i);
}
return sum;
}
int main() {
cin >> n >> m >> k;
double l = 0, r = 5.0;
while((r - l) > 0.0000001) {
double mid = (l + r) / 2;
if(check(mid) <= (1.0 * n) / m) {
r = mid;
} else {
l = mid;
}
}
printf("%.1lf", l * 100);
return 0;
}







Comments NOTHING