学习本文之前你需要:了解new关键字,懂结构体构造函数,懂分治的思想,会写二分查找。
线段树属于高级数据结构,主要有三大功能:
- 单点修改,区间查询
- 区间修改,单点查询
- 区间修改,区间查询
- 以上操作均只需要\(O\left( \log n \right) \)!
看上去好像没啥用,其实这玩意特别重要,尤其是在维护区间方面,你可以想像一下,如果直接使用普通的数组来计算一个区间的和,肯定是需要\(O\left( n \right) \)的复杂度,如果需要反复对区间进行操作,那这个速度会很慢。所以线段树就出世了,数据结构课上不讲这玩意可能是因为难度较高。
其实我也不知道这玩意为啥叫线段树,在我的印象中,线段、树,好像扯不上啥关系:


???
好吧其实真正的线段树不是这玩意,下面才是数据结构中的线段树:
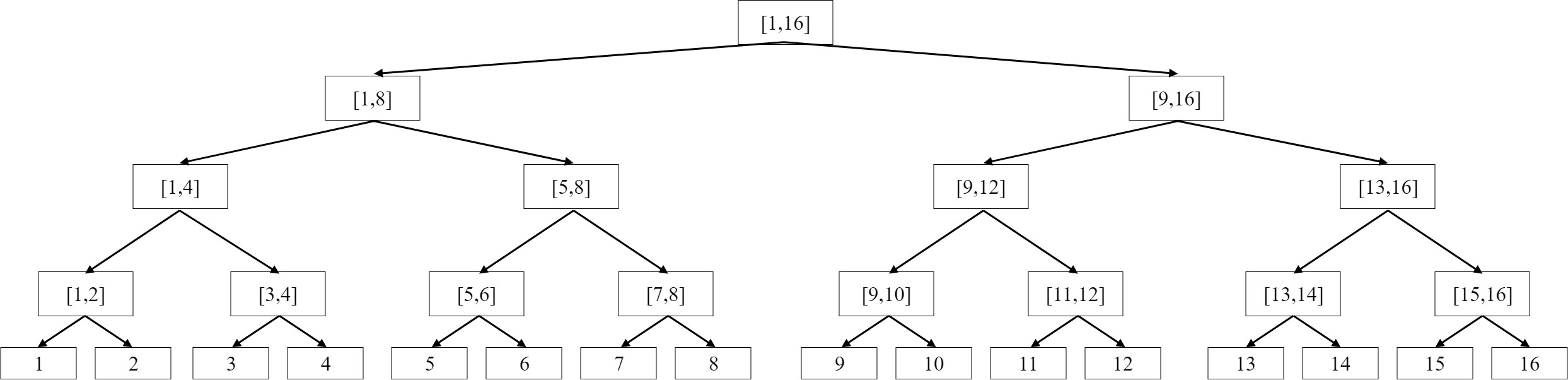
可以看到,我们所维护的整个序列是\(\left[ 1, 16 \right] \)。每一个叶子节点都表示一个单点,而非叶子节点都需要维护一个区间,比如根节点就表示维护整个区间。那么每一个区间中要维护那些东西呢,那就得看具体情况了,一般最常见的是维护区间和。比如根节点里面有一个值来表示这16个数据的和。
在开始之前先说明一下:我的代码风格和网上很多都不大一样,网上很多线段树都采用数组来模拟,但是空间消耗很大,需要提前开4倍的空间,洛谷上有人说有的题需要开8倍的空间才能过。所以我采用结构体指针加动态开点的方式写线段树(调了两天。。。)如果觉得我的代码不太好理解,推荐阅读这个。
首先来讲单点修改和区间查询
节点构造
我们使用结构体来存每一个节点需要维护的信息:
struct Node {
int l, r , value;
Node * left, * right;
Node(int l1 , int r1 , int v1 , Node * a, Node * b) { //构造函数
l = l1;
r = r1;
value = v1;
left = a;
right = b;
}
} *root;
int l 和int r表示当前节点所维护区间的左右端点,value当前节点所代表的区间和。Node * left , * right表示当前节点的左右孩子。下面结构体中的函数为构造函数。
建树
- 如果为叶子节点(l == r),直接new一个节点返回。
- 如果为普通节点,首先跟他的左儿子说:你自己负责你下面的孩子,并且把你的区间合告诉我。
- 再对右儿子说,你负责你下面的孩子,也把你的区间合告诉我。
- 那这个节点做什么呢?当然是负责将两个孩子的信息进行整合。
如果看懂了的话,代码应该不难理解:
Node * build (int l, int r) {
if(l == r) return new Node(l, r, a[l], 0, 0); //如果是叶子节点,直接返回一个新的节点,且左右儿子均为0(叶子没有儿子)
int mid = (l + r) / 2;
Node * left = build(l, mid); //递归构造左子树
Node * right = build(mid + 1 , r); //递归构造右子树
return new Node(l, r , left -> value + right -> value, left , right);
//通过左子树的value和右子树的value将父亲节点更新
}
区间查询
如果我们需要查询一个区间的和,我们需要怎么做呢?既然这个要查询的区间被分成了\(O\left( \log n \right) \)个节点,那么我们找到这些节点,并且把他们加起来就好了。
- 如果当前区间完全包含在要查询的区间中,直接返回这个区间的值
- 如果要查询的区间有一部分在左儿子中,那么搜索左儿子
- 如果要查询的区间有一部分在右儿子中,那么搜索右儿子
代码表示:
int find(int l, int r, Node * cur) { //l, r表示要查询的区间,cur是当前节点
if(l <= cur -> l && cur -> r <= r) //如果要当前区间完全包含在要查询的区间中,之积分返回
return cur -> value;
int mid = (cur -> l + cur -> r) / 2; //将当前区间分成两部分
int ans = 0;
if(r > mid) //如果要查询的区间有一部分在右儿子中,那么搜索右儿子
ans += find(l, r, cur -> right);
if(l <= mid)
ans += find (l, r, cur -> left); //如果要查询的区间有一部分在左儿子中,那么搜索左儿子
return ans; //将两边的结果返回
}
这几个if一定要看清楚!!
单点修改
单点修改还是比较简单的,如果我们要修改一个点的值,那我们不仅要修改这个点,其父亲、父亲的父亲......都需要被更新。比如说如果我们需要改16这个点的值,如图所示:
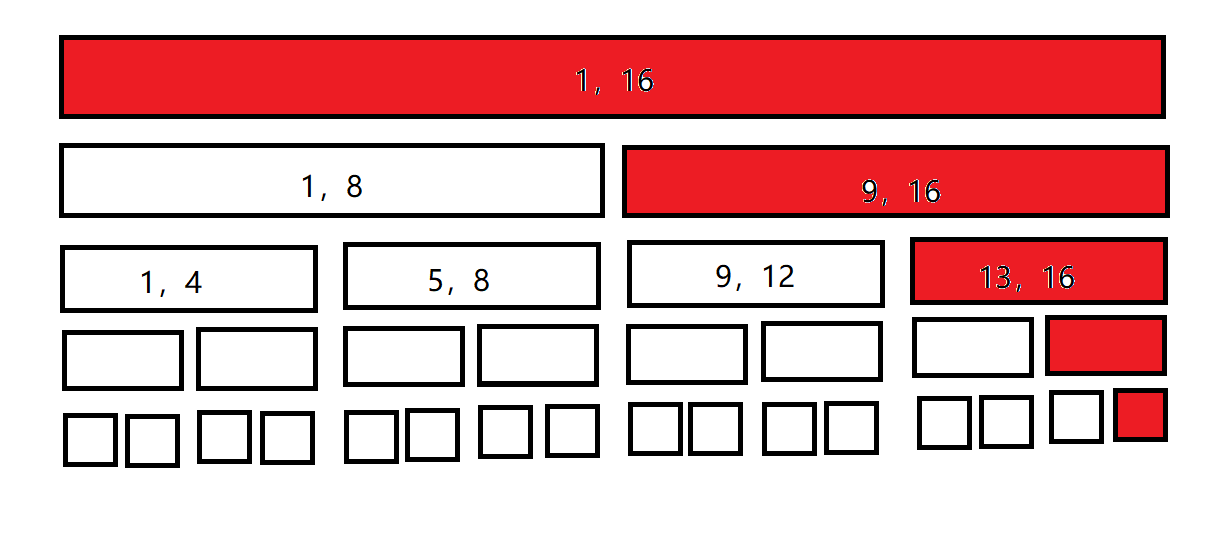
思路如下:
- 如果是叶子节点,直接修改
- 如果修改的位置在当前节点的左边,就去左孩子里面修改
- 如果修改的位置在当前节点的右边,就去右孩子里面修改
- 根据左右孩子的值更新当前节点
代码:
void modify(int x, int v, Node * cur) { //单点修改,将下标为x的地方加上v
if(cur -> l == cur -> r) //如果到了叶子节点,直接修改
cur -> value += v;
else {
int mid = (cur -> l + cur -> r) / 2; //如果不是叶子节点,开始递归处理左右子树
modify(x, v, (x > mid) ? cur -> right : cur -> left); //如果要修改的位置大于mid,进入right,小于进入left
cur -> value = cur -> left -> value + cur -> right -> value; //修改完孩子的值之后父亲的值需要被更新,很重要,别忘了!
}
}
完整代码:
#include<iostream>
#include<cstdio>
using namespace std;
int a[500010]; //存放区间的数组
struct Node {
int l, r , value;
Node * left, * right;
Node(int l1 , int r1 , int v1 , Node * a, Node * b) { //构造函数
l = l1;
r = r1;
value = v1;
left = a;
right = b;
}
} *root;
Node * build (int l, int r) {
if(l == r) return new Node(l, r, a[l], 0, 0);
int mid = (l + r) / 2;
Node * left = build(l, mid), * right = build(mid + 1 , r);
return new Node(l, r , left -> value + right -> value, left , right);
}
int query(int l, int r, Node * cur) {
if(l <= cur -> l && cur -> r <= r)
return cur -> value;
int mid = (cur -> l + cur -> r) / 2;
int ans = 0;
if(r > mid)
ans += query(l, r, cur -> right);
if(l <= mid)
ans += query(l, r, cur -> left);
return ans;
}
void modify(int x, int v, Node * cur) {
if(cur -> l == cur -> r)
cur -> value += v;
else {
int mid = (cur -> l + cur -> r) / 2;
modify(x, v, (x > mid) ? cur -> right : cur -> left);
cur -> value = cur -> left -> value + cur -> right -> value;
}
}
inline int read() {
int x = 0, ch = getchar();
int v = 1;
while(!isdigit(ch)) {
if(ch == '-')
v = -1;
ch = getchar();
}
while(isdigit(ch)) {
x = x * 10 + ch -'0';
ch = getchar();
}
return x * v;
}
int main(){
int n, m, l, r, opt;
n = read() ; m = read();
for(register int i = 1 ; i <= n ; ++i)
a[i] = read();
root = build(1, n);
while(m--) {
opt = read();
l = read();
r = read();
if(opt == 1)
modify(l, r, root);
else
cout << query(l, r, root) << endl;
}
return 0;
}

学到这里,你应该搞懂了线段树的基本操作,下面的内容较难。
区间修改与lazy_tag
如果我们要将一个区间整体进行修改,很常规的思想是for然后单点改,但是这样做了之后时间复杂度为:\(O\left( n\log n^2 \right) \),我们之所以使用线段树,就是因为它的速度比较快,显然这个时间复杂度是达不到我们的要求的,所以...既然要追求刺激,那就贯彻到底咯。
我们在这里引入一个新的元素:lazy_tag,可以叫它延时标记,也可以叫它懒标记,anyway,在学习这个lazy_tag之前,先看个故事:
A 有两个儿子,一个是 B,一个是 C。
有一天 A 要建一个新房子,没钱。刚好过年嘛,有人要给 B 和 C 红包,两个红包的钱数相同都是1元,然而因为 A 是父亲所以红包肯定是先塞给 A 咯~
理论上来讲 A 应该把两个红包分别给 B 和 C,但是……缺钱嘛,A 就把红包偷偷收到自己口袋里了。
A 高兴地说:「我现在有2份红包了!我又多了2 * 1 = 2元了!哈哈哈~」
但是 A 知道,如果他不把红包给 B 和 C,那 B 和 C 肯定会不爽然后导致家庭矛盾最后崩溃,所以 A 对儿子 B 和 C 说:「我欠你们每人1份1元的红包,下次有新红包给过来的时候再给你们!这里我先做下记录……嗯……我欠你们各1元……」
儿子 B、C 有点恼怒:「可是如果有同学问起我们我们收到了多少红包咋办?你把我们的红包都收了,我们还怎么装?」
父亲 A 赶忙说:「有同学问起来我就会给你们的!我欠条都写好了不会不算话的!」
这样B、C才放了心。
故事出自——oi-wiki,侵删
再举一个具体的例子:如果我们之前反复修改过1到4号节点的值,但是我们再查询的时候,只涉及到了9到16这个区间,也就是说我们修改的值并不会被用到,那这个时候,我们就完全可以打上一个标记,而不去修改它的值。什么时候修改呢?当然是等到要用到它的时候了。
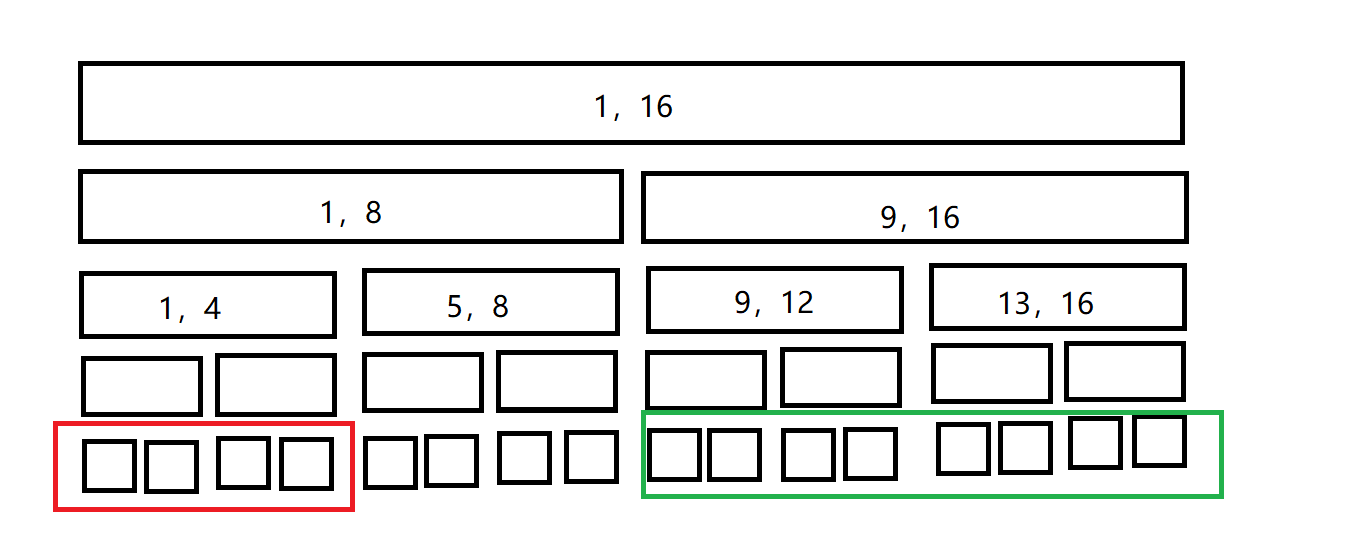
我们首先更改我们的结构体,每个节点中加上一个tag标签。
struct Node {
int l, r, value, tag;
Node * left , * right;
Node (int l1 ,int r1 , int v, Node * a , Node * b) {
l = l1;
r = r1;
value = v;
left = a;
right = b;
tag = 0;
}
} * root;
初始状态下tag肯定都是0。
区间修改:
- 我们在节点上维护一个标记,代表这个节点被加了多少值
- 查询的时候,对于每个经过的节点,下放标记到其儿子
- 这样我们查询的时候还是查询log个节点,与之前不同的是,每个节点有可能被整体加了一个值
标记下放:

我们将父亲的标记下方到它的儿子身上,同时,也需要将标记对区间的影响作用到区间上。比如:一个区间当前的tag为114514,这个区间包含了1919个数(r-l+1)也就是区间长度,那么value += 114514*1919,因为每个数都需要加上114514,一共是1919个。(这块需要好好理解,有点难理解)
所以我们标记下放的代码可以写成:
void pushdown(Node * cur) {
if(cur -> tag == 0) return;
if(cur -> left) { //如果不是叶子节点
cur -> left -> tag += cur -> tag;
cur -> right -> tag += cur -> tag;
cur -> left -> value += (cur -> left -> r - cur -> left -> l + 1) * cur -> tag;
cur -> right -> value += (cur -> right -> r - cur -> right -> l + 1) * cur -> tag;
} else { //如果是叶子节点,直接加上tag
cur -> value += cur -> tag;
}
cur -> tag = 0;//标记清空
}
打标记与标记对区间的影响搞懂了之后(这块可以多看几篇博客和视频,这就是线段树的精髓),我们再来考虑如何对区间进行修改:
void modify(int l ,int r , Node * cur , int v) { //将l到r这段区间增加v
if(l <= cur -> l && cur -> r <= r) {
cur -> tag += v; //打标记
cur -> value += (cur -> r - cur -> l + 1) * v; //增加的值对区间的影响
return;
}
pushdown(cur); //下面要用到儿子,所以要进行标记下传
int mid = (cur -> l + cur -> r) / 2;
if(mid >= l) //这块和区间查询类似
modify(l, r, cur -> left, v);
if(r > mid)
modify(l, r, cur -> right, v);
cur -> value = cur -> left -> value + cur -> right -> value; //别忘了更新当前区间。
}
由于使用了tag,所以区间修改也需要作出相应的变化:
int query(int l, int r , Node * cur) {
if(l <= cur -> l && cur -> r <= r)
return cur -> value;
pushdown(cur); //由于之后会用到左儿子和右儿子,所以需要将标记下传
int mid = (cur -> l + cur -> r) / 2;
int ans = 0;
if(l <= mid)
ans += query(l, r, cur -> left);
if(r > mid)
ans += query(l, r, cur -> right);
return ans;
}
全部的代码:
#include<iostream>
#include<cstdio>
using namespace std;
#define int long long
int a[500005];
struct Node {
int l, r, value, tag;
Node * left , * right;
Node (int l1 ,int r1 , int v, Node * a , Node * b) {
l = l1;
r = r1;
value = v;
left = a;
right = b;
tag = 0;
}
} * root;
Node * build(int l , int r) {
if(l == r)
return new Node(l, r, a[l] , 0 , 0);
int mid = (l + r) / 2;
Node * left = build(l , mid);
Node * right = build(mid + 1, r);
return new Node(l, r, (left -> value + right -> value) , left , right);
}
void pushdown(Node * cur) {
if(cur -> tag == 0) return;
if(cur -> left) { //如果不是叶子节点
cur -> left -> value += (cur -> left -> r - cur -> left -> l + 1) * cur -> tag;
cur -> right -> value += (cur -> right -> r - cur -> right -> l + 1) * cur -> tag;
cur -> left -> tag += cur -> tag;
cur -> right -> tag += cur -> tag;
} else { //如果是叶子节点,直接加上tag
cur -> value += cur -> tag;
}
cur -> tag = 0;//标记清空
}
int query(int l, int r , Node * cur) {
if(l <= cur -> l && cur -> r <= r)
return cur -> value;
pushdown(cur);
int mid = (cur -> l + cur -> r) / 2;
int ans = 0;
if(l <= mid)
ans += query(l, r, cur -> left);
if(r > mid)
ans += query(l, r, cur -> right);
return ans;
}
void modify(int l ,int r , Node * cur , int v) { //将l到r这段区间增加v
if(l <= cur -> l && cur -> r <= r) {
cur -> tag += v;
cur -> value += (cur -> r - cur -> l + 1) * v;
return;
}
pushdown(cur); //下面要用到儿子,下传tag
int mid = (cur -> l + cur -> r) / 2;
if(mid >= l)
modify(l, r, cur -> left, v);
if(r > mid)
modify(l, r, cur -> right, v);
cur -> value = cur -> left -> value + cur -> right -> value; //update
}
int read() {
int x = 0 , ch = getchar() , v = 1;
while(!isdigit(ch)) {
if(ch == '-')
v = -1;
ch = getchar();
}
while(isdigit(ch)) {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * v;
}
signed main() {
int m , n, opt, x, y, k;
n = read() ; m = read();
for(int i = 1 ; i <= n ; ++i) {
a[i] = read();
}
root = build(1, n);
while(m--) {
opt = read();
if(opt == 1) {
x = read();
y = read();
k = read();
modify(x, y, root, k);
}
else {
x = read() ; y = read();
cout << query(x, y, root) << endl;
}
}
return 0;
}

其实线段树可以在一个区间内可以维护的东西有很多,不一定只是区间的和,还可以维护区间乘、区间最小值、区间最大值之类的,但是如果基础的都弄懂了,再看那些东西还是不难的。







Comments NOTHING