23张宇八套卷（一）

本来按照原定的计划，这周应该进行模拟卷的复盘总结，但是周末机构组织模拟考试，想着好像没有几次机会就要上考场了，所以今天上午去模拟教室做了一套卷子。其实张宇的卷子我很早就打印了，毕竟肯定是要做的，只是时间的问题。

这张试卷做的并不好，三个小时拉满还是没做完，选填不仅计算量大而且有好几道题也都比较难想，大题的计算量除了第一道题以外其他题目的计算量也都挺大的，也有超级难想的压轴题。

总的来说，客观评价这张试卷，我感觉可以提前体验一下考场上的感受，至于分数我觉得实际上是没有什么参考意义的。

下面开始复盘：

第一道题这么明显的cxk真的好吗？？好像某年的真题也是这几个字母。。这道题还是比较简单的，只不过我们平常记的等价无穷小一般都是$ln(x+\sqrt[]{1+x^2} )\sim x$，至于高阶以上的就用的比较少，但是知道$ln(x+\sqrt[]{1+x^2} )$是一个奇函数，那么就肯定在AB里面选了，后面就用洛必达判断就行。

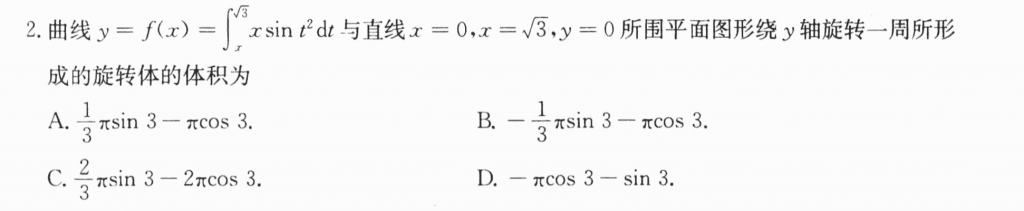
第二题还好，先套公式，然后对于这个二重积分，首选交换次序，然后再计算就不难了。

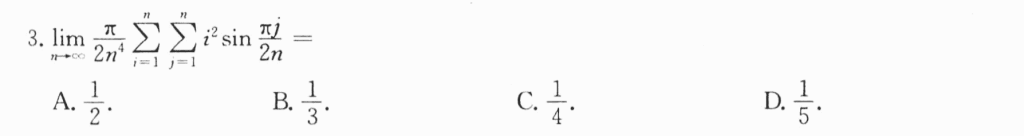
利用二重积分的定义，也不难

这道题的其实思路比较简单，比较麻烦的点就在于判断后面$ln(1+x)-\frac{arctanx}{1+x}$的符号，可能比较好想的方法是直接求导分析单调性，但是求完导数之后发现很困难，答案的方法是在等式的左右两边同乘$x+1$，然后再判断一阶导数的符号就方便了。

还有一个比较方便的方法是直接对等式进行放缩$$ln(1+x)-\frac{arctanx}{1+x}>\frac{x}{1+x}-\frac{arctanx}{1+x}(x>0)$$再根据$x > arctanx$，就可以判断符号了，这个方法主要在于比较难想。

这是一道难度很大的选择题，我在做的时候想的太少，所以选错了。。$F(x) > f(x) \to \frac{1}{f(x)} > \frac{1}{F(x)}$，根据大的收敛小的收敛就可以推出充分条件了，但是必要条件我想了一会发现没什么比较好的思路就以为证明不出来。。水平着实有限。

答案的方法是构造了一个等式：$\frac{1}{f(x)} = \frac{1}{f(x)} -\frac{1}{F(x)} + \frac{1}{F(x)}$，然后分析$\frac{1}{f(x)} -\frac{1}{F(x)}$的敛散性，发现是收敛的，那么左右两边的$\frac{1}{f(x)} = \frac{1}{F(x)}$就同敛散了，所以是充要条件。

这道题也是难题，首先要用把极限号去掉，写出$f(x, y)$的表达式，然后再转换成极坐标来判断（开眼界了）

裸的二重积分，交换次序老朋友了

一道很经典的题，这道题要注意的细节就是要区分清余子式和代数余子式，然后按照行列式的展开定理构造一个新的行列式，最后行列式的值就是这个式子的值。

第九题不难，把两个初等矩阵写在一左一右发现是可逆的关系，那么A矩阵和所给矩阵就是相似的关系，那么迹相等，所以很快就能把A选出来。

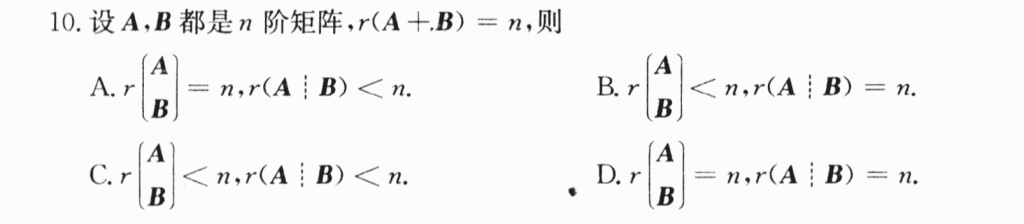
这道题不难，我看答案好像搞了分块矩阵的乘法，但实际上我感觉不用整那么复杂：$n = R(A + B) <= R(A) < n$，同样对B矩阵也可以这样操作，那么就可以知道A和B矩阵里面一定是有一个矩阵是满秩的，所以拼起来肯定也可以推满秩了。

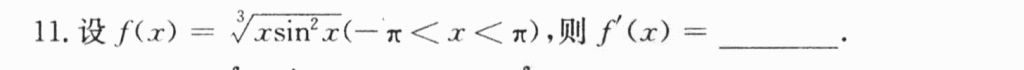
第十一题真坑，我考虑到了是否要分$x=0$，但是我求完导后验证了$\lim_{x \to 0}f'(x) = f'(0)$，发现是连续的，所以就没特意分区间。。。原来可去间断点也要分区间，又是一个小细节。

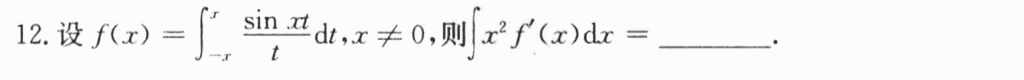
这道题我一开始方向错了，看到被积函数里头有个$f'(x)$就忘d里头凑，然后用分部积分，结果发现啥也搞不出来。然后就换方向，先把$f'(x)$求出来，然后带到积分里头计算，就算出来了。

这道题计算量也挺麻烦的，不过我在其他文章里面也反复提到过，像这种比较麻烦的参数方程求二阶导数一般用那个定义会比较简单一些。

这道题不难，就分离参数就好，难度不大，但是我还是做错了，忘记考虑$x<0$的情况了，一下五分没得了，血亏。

物理应用，无力题，pass了

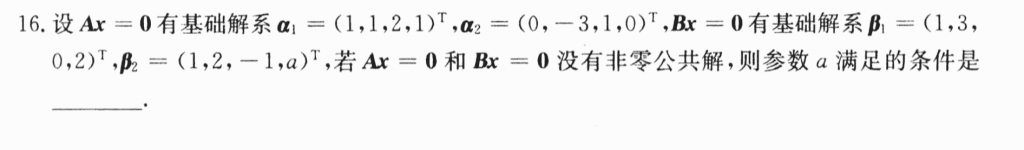
因为他们没有非零公共解，也就是说解向量之间是线性无关的，所以把这四个向量拼起来，然后初等变换，只要让他们满秩就好了。

这道题也是有小细节的，主要是要发现方程里头有个完全平方：$x^2-2x+1$，然后直接洛必达后再化简就好算了。

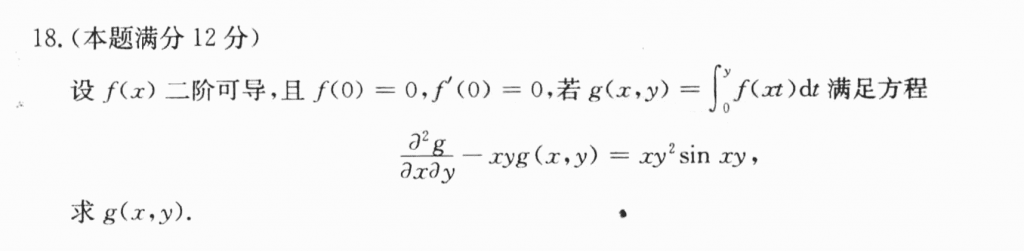
这道题我感觉挺复杂的，首先要意识到$\frac{\partial ^2g}{\partial x\partial y} = \frac{\partial ^2g}{\partial y\partial x}$，然后求偏导后带到这个式子里头化简，再令$xy = u$，就可以得到一个一元的微分方程，解这个微分方程可以把$f(xy)$解出来，然后两边从0到y积分，就能把$g(x, y)$弄出来了。

比较基础的物理应用题，第一问要求时间，那么肯定要先求体积，然后除以Q就好了，$y = \frac{1}{a}x^2$，绕y轴的旋转体体积，直接套公式。

第二问不难，主要是公式：$W=FS=mgS=\rho v g S = \rho \pi x^2 dy g (a - y)$，然后积分就行。

这道题第一问我把式子列出来以后就直接把方程弄出来了，因为曲率半径是一个固定的数，那么肯定是圆，然后再根据所给条件就能把圆的方程给推出来。

第二问的话可以用一手对称，积分区域是关于$x = 1$对称的，那么$\iint_{0}^{2} (x-1)d\sigma = 0$，所以可以再被积函数里头凑$xy - y + y=y(x-1) + y = y$，然后再算就比较方便了。

这道题也太难了。。第一问想了半天没想出来，第二问的话就先从$F_1, F_2$依次往后推，然后总结规律再带到极限里头计算，最后要用第一问的结论放缩，用夹逼定理。

这道题前两问细心一些应当问题不大，主要是第三问如果没见过的话我感觉还是很难想到的，需要结合前两问的结论，根据第一问可以知道用$C$矩阵可以把$f(x_1, x_2, x_3)$进行标准化，然后第二问知道用$CQ$可以把$g(x_1, x_2, x_3)$进行标准化，所以结合一下就发现$CQ$可以把他俩同时标准化。

复盘结束，码字较快，如果有什么问题欢迎在评论区与我交流，感谢阅读！