这套试卷是今天晚上做的,做的时候困的要命,状态不太行,写了165分钟才写完,不过好在这套试卷的难度不大,计算量也还好,不然可能真就做一半就放弃然后跑去睡觉了hhh。
下面开始复盘:

第一题我用的拉格朗日,直接证明A是正确的,答案没有提供过程,我在这里写一下:
$$\lim_{x \to +\infty } \frac{f(x)}{x} = \lim_{x \to +\infty}\frac{f(x) - f(x_0) + f(x_0)}{x}= \lim_{x \to +\infty} \frac{f'(\xi)(x - x_0) + f(x_0)}{x} = l$$这样就大概证明出来了。
BCD选项答案都给了反例,感觉遇到$f(\infty), f'(\infty)$的情况,首选应该考虑$\frac{1}{x}$

这道题就比较基础了,垂直渐近线和斜渐近线
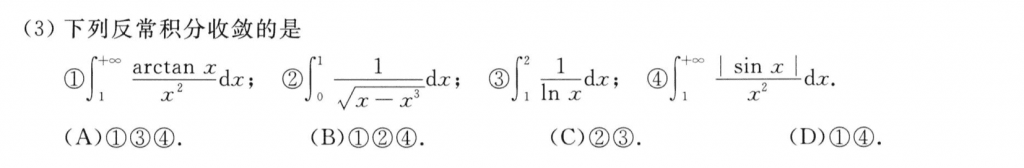
第三题也是比较基础的题,
首先第一个可以直接把arctan放缩掉,然后在根据大的收敛,小的一定收敛可以证明1是收敛的
第二个分别分析$x \to 0, x \to 1$的情况
第三个可以作等价无穷小变形再判断,$\lim_{x \to 1} lnx = \lim_{x \to 1}ln(1 + x - 1) \sim x-1$
第四个也可以直接放缩,$sinx<1$
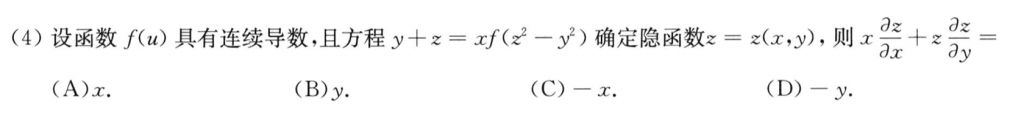
这道题虽然没什么难度,但是我感觉计算量还是有点,中间有一个步骤需要用方程$x + z = xf(z^2 - y^2)$把z带换掉再化简

基础题
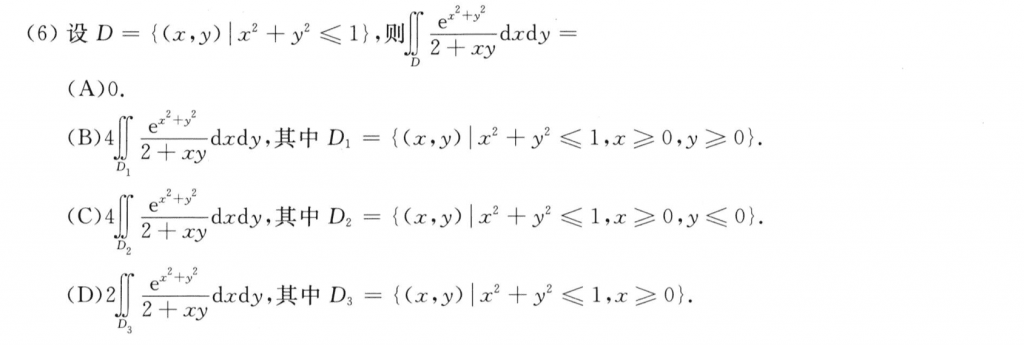
这题我还瞪了半天,主要是对$y=-x$对称的性质不太熟悉,具体的分析等我用pad画图表示,mac的画图太垃圾了。

第七题也不难,考察$1^\infty$
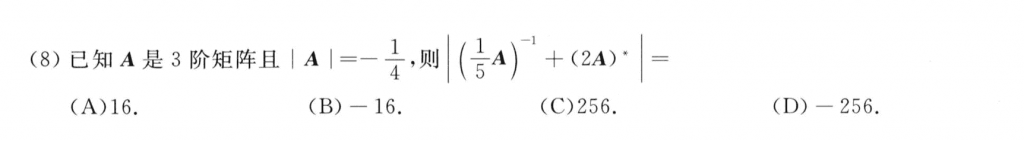
第八题要想到先给要求的这个式子乘上一个A的行列式然后就可以把$A^{-1}, A^*$都搞掉,再化简就好操作了,不过要记得最后的结果要除以A的行列式

果然晚上做题脑子不清醒,直接$Ax = 0$有非零解就完了

其实对于这种不需要求出具体特征值的规范性或者标准型,用配方法应该是比较快的,因为有时候题目就是会卡特征值,让这个计算过程很麻烦或者根本算不出来。当然这道题还算是比较友好的,我是直接推着做的,先把二次型矩阵A写出来,然后根据tr(A) = 0就可以排除A和C了,然后秩为2,那么肯定有零特征值,所以可以把B排除。

基础题

刚拿到这道题的第一想法肯定是考虑周期性什么的,发现都没有,然后就要考虑其他的办法了,像这种积分和极限混在一起的题,一般有几种解决方法,第一种能积出来肯定先积出来再算极限,如果不能积出来,那么考虑积分第一中值定理,把一部分搬到外面,然后留在里面的不变号,然后把积分计算出来以后再算极限,还有就是像这道题所用到的手法,把$sinx$放缩,然后用夹逼来算。
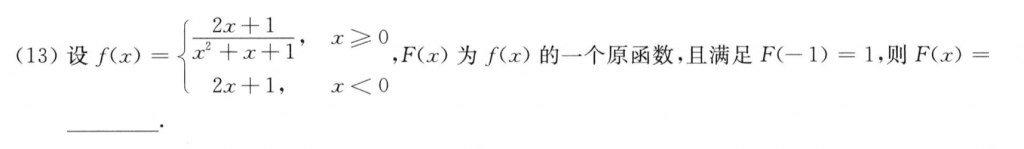
先分段求F,然后根据$f(x)$可积,那么$F(x)$连续可以把$C_1, C_2$的关系式找到,再根据$F(-1) = 1$就可以把参数$C_2$给确定下来。

套公式基本题

根据齐次方程通解来推齐次方程,然后再把x带到方程里面,就可以得到非齐次项了。

这题是真坑啊,我在$A_{11} + A_{22} + A{33}$以及$A_{11} + A_{12} + A_{13} + ...$之间纠结,然后想到如果是后者的话,那应该有两个求和符号,所以就果断选了前者。。结果就被坑了

这道题第一问基本就是送分题,第二问的话,我用的是极坐标算的,还是有些麻烦,答案又用了换元,和某道真题如出一辙,我依旧硬算,其实硬算也还好,就$\frac{sec^3t}{tant}$我就在这一步卡了一会,然后想到可以把分子上的$sec^3t$分成平方和一次方相乘,然后平方那一项可以联系$tan^2t$,再积分就简单了。
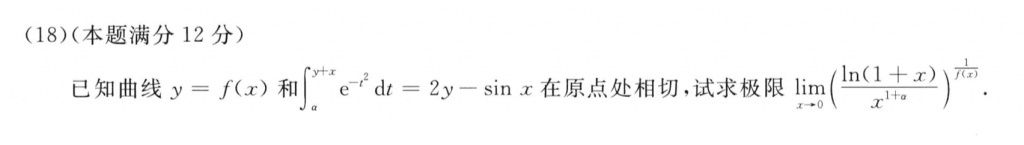
这道题也不简单,考$1^\infty$
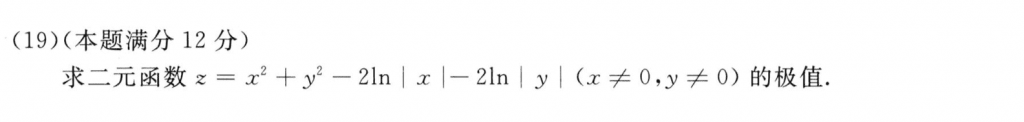
基础题
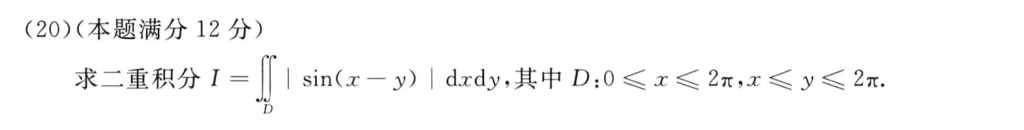
这道题做过好多遍了,李正元全书,880上都有,主要是分块积分,sin的符号就行了。

这道题我感觉有点难,我用的单调性的方法,求了好几阶导才证明出来。。

这道题也比较简单,第一问就$\alpha_1, \alpha_2, \alpha_3$线性相关,然后他们的行列式为零,就可以把a搞出来。
第二问也简单
第三问是一个套路题,先用$\alpha_1, \alpha_2, \alpha3$把$\beta$表示出来,然后再用$A\alpha=\lambda \alpha$来操作就简单了。







Comments NOTHING