这张试卷是今天晚上做的,趁热打铁,来博客复盘一下,明显感觉这张卷子做起来比2009年的要压力大了一些,但是也能接受,晚上的状态,两个小时左右就做完了。
现在开始复盘:

第一题实际上不难的,先约分,然后发现要么$x=-1$或者$x=0$是可能的无穷间断点,然后算一下极限发现$x=0$的那个点极限存在,所以无穷间断点就只能是$x=-1$

第二题实际上还是比较麻烦的,在线代里头有一个结论:

也就是说如果是非齐次方程的解,那么前面的系数之和为1,如果是齐次方程,那么前面的系数之和为0,完全可以用到这个题里面,那么答案就很容易出来了。

第三题也不难,就切点相同,切点处的斜率相同,然后就可以求出来了
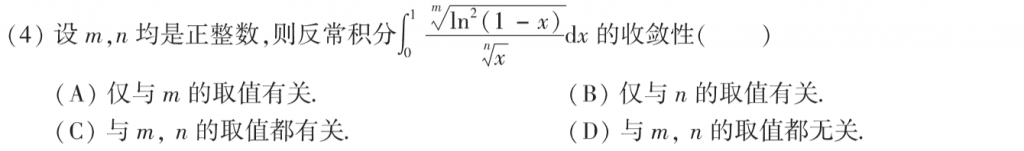
第四题难的,不过武忠祥强化就讲过这道题,所以难度也就不大了,首先考察$x \to 0$的部分,通过等价无穷小等化简的形式可以得到$\frac{1}{n}-\frac{2}{m}<1$,而$m$和$n$都是正整数,$\frac{1}{n}-\frac{2}{m} < \frac{1}{n} < 1$,所以趋于零的这个就与$m$和$n$无关了,然后考察$x \to 1$,这个时候除以一个$\frac{1}{(1-x)^\alpha}$的东西,$0<\alpha<1$,然后可以证明这个极限(比较审敛法)趋于零,而$\frac{1}{(1-x)^\alpha}$收敛,所以ln那个就收敛,又与$m,n$无关了。

第五题这种抽象函数用公式法会比较简单
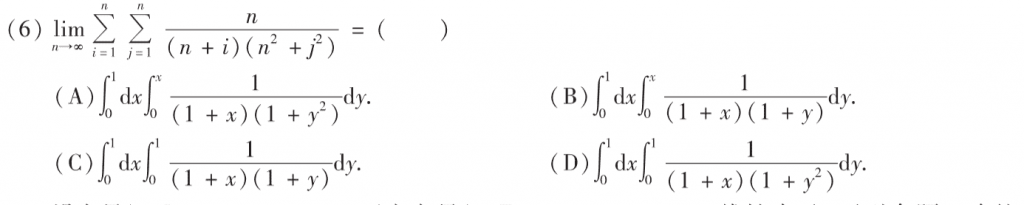
第六题看着复杂,实际也不难,就是两个定积分的定义

第七题也简单

关于第八题我想说的一点就是题目给了$A^2+A=0$,那么就可以推出$\lambda^2+\lambda=0$,所以$\lambda$只能取0或者-1,没有可能取其他的值,因为其他的值都不满足这个方程,再根据秩就可以知道有几个-1了
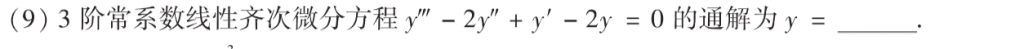
基础题,去年好像考了个差不多的

基础题

这题我做错了,ln的那个展开式忘记去掉首项1了,导致最后和答案差了个符号,四分一下就没了。。
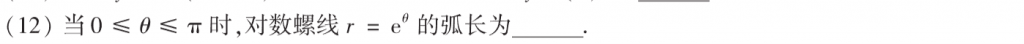
也简单,套公式就好了

这个题就复合函数求导,把对角线的方程写出来$u = \sqrt(l^2+w^2)$,然后两边同时对$t$求导就好了
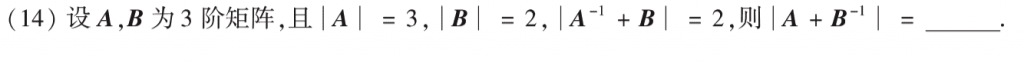
第十四题是李永乐强化课的经典题了,两边贴单位矩阵变形

第十五题也不难,首先可以知道这是个偶函数,然后求导,对于一阶导直接分析正负就好了

这题也简单,第一问就经典的不等式放缩,然后第一问都给不等式了,第二问肯定要考虑夹逼。

这题不难,计算量也还好

这题看着难,其实非常简单,直接对椭圆建立我们高中常用的那个坐标系,然后质量就是密度乘体积,体积的话就底面积乘高,底面积就$2x \times dy$,然后高就是那个$l$

第十九题武忠祥的强化课也讲了个比较简单的方法,就是把$x$和$y$用$\xi, \eta$表示出来,然后再算
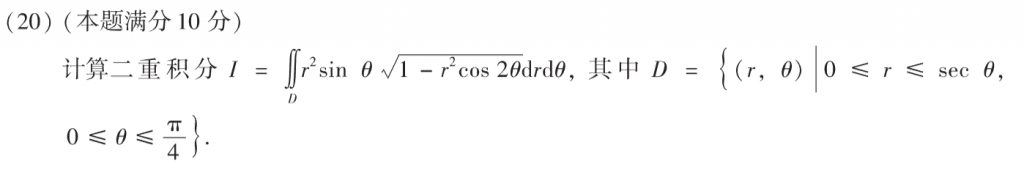
第二十题的方法就是把极坐标方程化为直角坐标方程计算,难度不大。

第二十一题也不难,刚开始还想了会,然后就先考虑一个部分,对于$f'(\xi) = \xi^2$,我们可以构造辅助函数$F(x) = f(x) - \frac{1}{3}x^3$,然后在区间$(0, \frac{1}{2}), (\frac{1}{2}, 1)$用两次拉格朗日之后联立方程组就出来了。

基础题

这题也不难,根据$A\alpha=\lambda \alpha$就可以得到a了
然后$A$就出来了,求三个特征值和三个特征向量就ok
复盘结束,码字较快,如果有问题可以在评论区留言,感谢阅读。











Comments NOTHING