这张卷子是昨天下午做的,上午搞专业课去了,不得不说,做了超越之后再做真题就像切瓜砍菜似的。。很快就做完了,正确率也还可以。
下面开始复盘

第一题主要是要看清楚题目要求可去间断点,我差点选了D。。
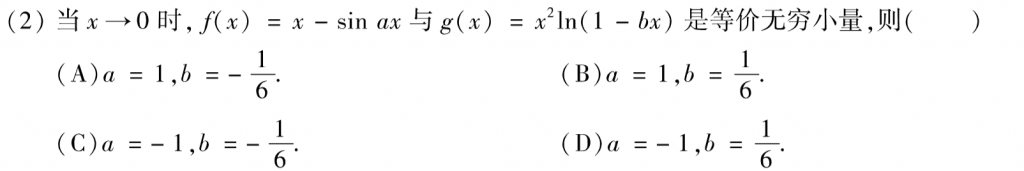
第二题也不难,可以直接看出来
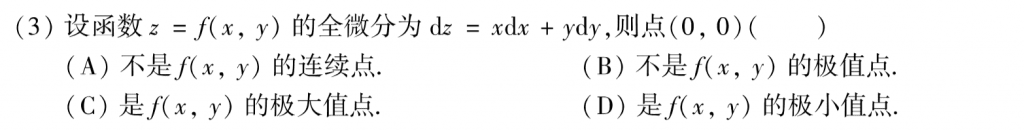
第三题可以把两个偏导搞出来,然后再求二阶偏导,用$AC-B^2$判断极值点

第四题画个图就出来了,不难,基础题

第五题我做错了,本来之前还专门复习过这个曲率圆,结果又给忘了,总的来说就是研究一个函数在一个点的性质,可以用曲率圆上的点来代替研究,然后这道题还是挺有意思的。
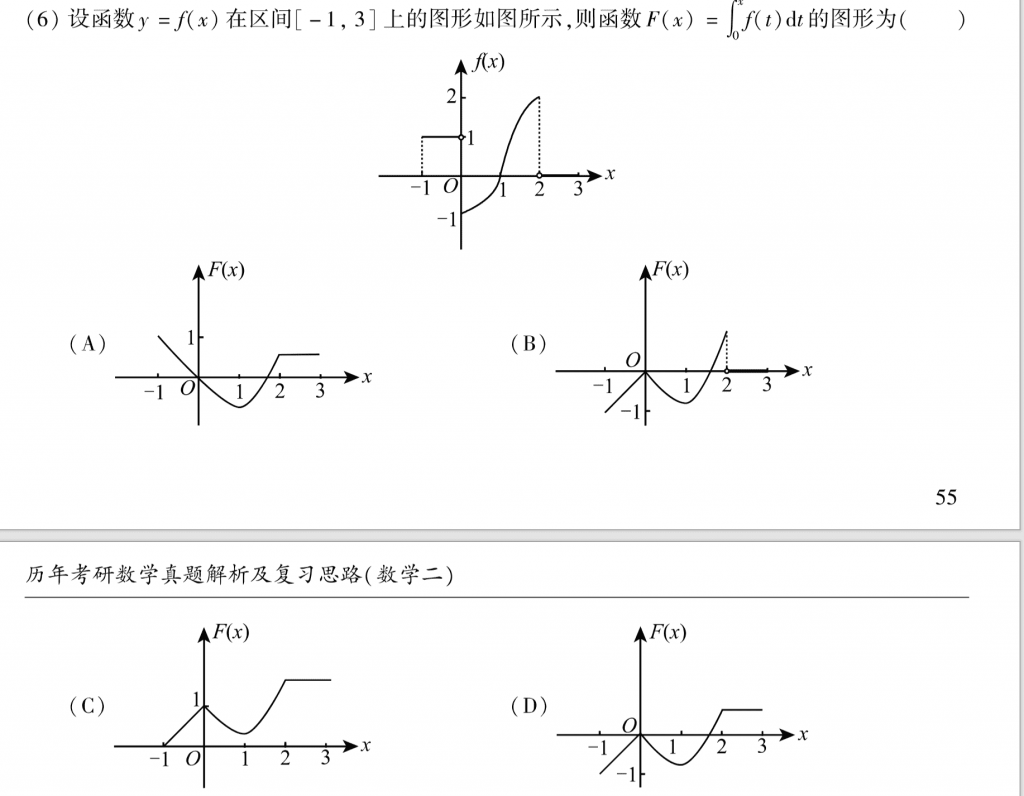
第六题我也给搞错了,没有意识到在小于零的部分,那个上限是小于零的,所以前面的那一段应该是个负的。。

这道题也做过不少次,$AA^*=|A|E$,这里的A可以是一个分块矩阵

$$Q=P\begin{bmatrix}
1 & 0 & 0\\
1 & 1 & 0\\
0 & 0 &1
\end{bmatrix}$$然后整体带入计算

基础题
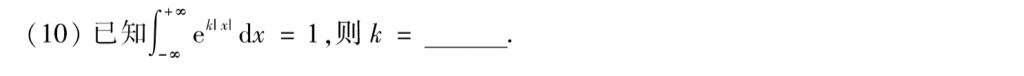
先把积分切断,去绝对值,然后分别计算就行了,既然最后的结果是一个值,那么k可以推出肯定是小于零的,所以那俩无穷直接扔掉就行,然后就可以把k整出来了

这题不用整那么多有的没的,把$sinnx$凑到后面,然后前面有一个$\frac{1}{n}$,趋向零,然后后面那俩有界,就可以推出是0了。

基础题
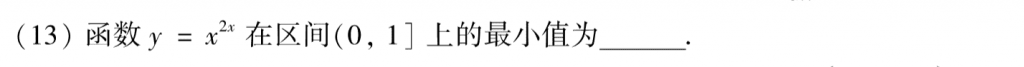
基础题

$\beta^T\alpha$实际上就是$\alpha\beta^T$的迹
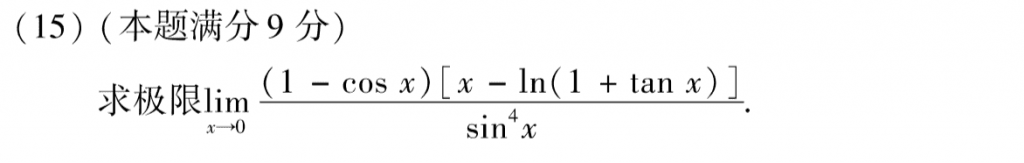
基础题,对于$x-ln(1+tanx) = x-tanx + tanx - ln(1+tanx) = -\frac{1}{3}x^3+\frac{1}{2}tan^2x=-\frac{1}{3}x^3+\frac{1}{2}x^2$
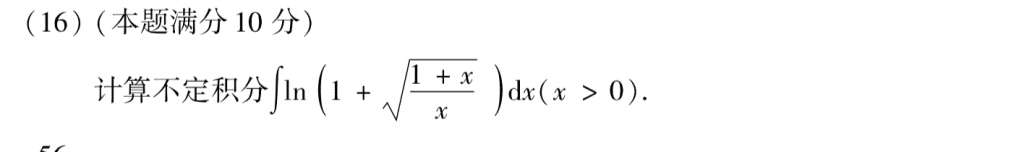
根号换元,然后中间有一步分式挺麻烦的,要么部分分式分解,要么凑了之后约分

17题也不难,基础

套公式就完了

中心不在圆心的圆可以可以通过平移换元,搞到原点

曲线光滑,那么就是在分段点处连续,并且左导数等于右导数,可以把两个参数确定下来,武忠祥的严选题上有这道题,印象深刻。

对于拉格朗日中值定理证明,构造辅助函数$F(x) = f(x) - \frac{f(b)-f(a)}{b-a}(x-a)$,比较简单,可以证明$F(a)=F(b)$,然后用罗尔定理就出来了。
第二问就用导数定义,然后拉格朗日一次,就可以了。

这题挺有意思的,我还以为要用特征值特征向量的方法来求$\xi_2, \xi_3$,但是搞了一会发现搞不出来,就放弃了,直接暴力解方程,没想到答案也是这样操作的。
第二问的话可以用定义,但是要意识到$A\xi_1=0$,这个还是比较难想的,我就直接用的行列式

这题也简单,无非就是带参数的特征值,不稀奇。
第二问的话,根据规范型可以知道有一个特征值是零的,然后另外两个特征值都大于零,因此可以对第一问中求出来的那个特征值排个序,然后把最小的那个设置为0,就可以把a的值求出来了。
感谢阅读,码字较快,如果有什么问题,可以在评论区给我留言!







Comments NOTHING