昨天晚上做了一套超越,结果就把心态给做崩了,做题时间大概两个半小时,选填难度很高,大题相对来说还好,计算量是偏大的,我做错了好多。。以后再也不晚上写模拟题了,脑子不清醒的。
下面开始复盘。

第一题我就觉得是一道比较难的题,1和2应该比较好看出来,对于3的话其实也不难,因为$F(x)$在(0, 1)是连续的,所以只需要考察$\lim_{x \to 0}F(x) \exists$,显然是存在的,因此可以说明有界。对于4的话,就对$F(x)$求导,然后用一次积分中值定理,就可以得到$F(x)$的单调性了。

第二题应该就是一个结论,以前听汤家凤讲过伽马函数,没记错的话应该是这个,也不难,就是凑分部积分,然后可以得到一个递推关系,根据答案的设置,很容易把B给选出来。

这题是真难,我感觉好像每个选项都是对的,答案的那个反例我是真想不到,这种比较厉害的反例可以积累一下:

然后就把ABC排除了,关于证明D正确,我的过程和答案其实是一样的,但是不知道为什么脑子不清醒,没有意识到$f(0) \ne 0$,然后就没选出来。。
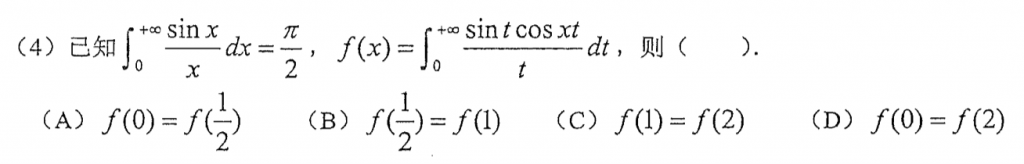
毫无疑问,又是一道难题,其中$f(0)$和$f(1)$应该是比较好推的,一个直接就是原极限,另一个是sin二倍角,换元就好了,对于$f(\frac{1}{2})$,答案用了积化和差!鬼知道这玩意,还想了半天,要是知道要用到这个这道题直接放弃,$f(2)$也不好推,答案好像又用的积化和差。。。离谱

这道题我又脑子不清醒选错了,偏导存在什么都推不出来,但是可以推出$f(x, y)$在$(x_0,y_0)$的十字架是连续的,也就是本题的B选项,我错选了C,C需要的前提是$f(x, y)$可微。

这个题不难,根据积分区域的性质可以得到$x > y$,然后他们都是小于1的,所以可以推出ln那个是小于零,肯定就是最小的了,其他两个的话,可以尝试换一手元,令$x-y=t$,然后比较$e^{t^3}$和$t^3$的大小就好了。

$Ax=0$的解可以用$\xi _1,\xi_2$和线性组合表示出来,用方程组的语言来说就是:$\xi_1 x_1+\xi_2 x_2 = \alpha$,把增广矩阵画出来,然后判断是否有非零解就好了。

这道题还是比较简单的,(1)经过初等行变换后的特征值就变了,所以我们在求特征值的时候,一定是要根据原矩阵来求的,要不然就有一个非常bug的方法了hh。(2)的话主要就是非零特征值应该是一个。(3)就是矩阵P应该要可逆
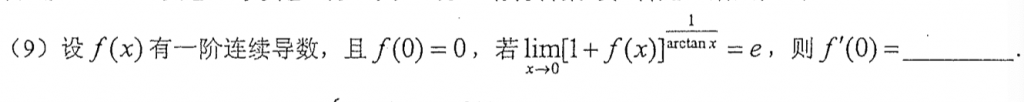
三部曲秒杀了

这题也是基础题,但是我犯了一个超级低级的错误,就类似:$\frac{1}{2} = \frac{2}{4}$,然后我就:$1=2, 2=4$了。。。还是要认真一些。。

这题不难,但是结果挺离谱的,不知道为啥还要求个平方和。。还以为自己算错了,反复验证了几遍之后才发现没问题。

基本的分部积分题目,不难

也不难,就分区间然后求导找驻点。。我又又又算错了$$\sqrt{t}=\frac{1}{2} \to t = \pm \sqrt{\frac{1}{2} }$$
细心细心

本质就是方程组求解,不要被迷惑住了,简单题。

这题也不难,就洛必达,然后泰勒,或者导数定义反复横跳就完事了

证明是拐点就只需要证明在二阶导数两侧异号就好了,然后第二问的话,我还想了一会,实际也很简单,分母先变一下x,前面那个$f'(x)$可以凑一个导数定义,然后后面那项也可以凑一个导数定义,然后就可以得到在0点处的三阶导数不为零了,再根据第一问的结论,就可以把拐点给推出来。
(话说这种结论性质的东西考研应该可以直接用吧,为啥要单独考呢?)
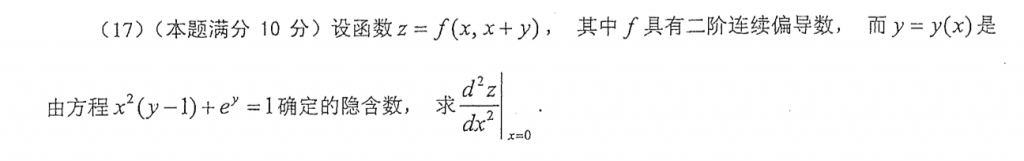
基础题,注意好计算细节就好了。

这题也很简单,根据x分区间然后把那个min给去掉,然后就变成了变限积分,然后就可以开始愉快的求导与解微分方程了。(注意在过程中推f(0)啥的信息)
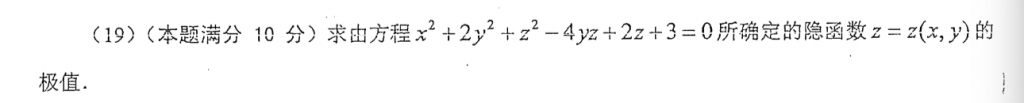
这应该是我第一次做出完整的隐函数的极值问题,本身这种题好像不是很多,然后武忠祥讲义上的那道例题计算太过繁琐,所以只学了个思路,没有付诸于实践,这道题我感觉可以作为隐函数求极值问题的例题了,好题!

答案好像搞的挺麻烦的,我没怎么看,因为我感觉我的过程应该没有什么问题,第一问我直接用单调性做的,把b都改成x,然后证明$F(b)>0$就好了,$F(a) = 0$,所以问题又转化为了证明$F'(x)>0$,这个就很简单了,中间要用一次拉格朗日。
第二问也不难,我直接用泰勒写的,把$f(x)$在$x = \frac{1}{2}$处展开,拉格朗日余项就是这个$\xi$,然后从a到b积分,第一项可以用题目的条件,第二项那个一次项积分出来为零,然后可以证明这个$f''(\xi)=0$了
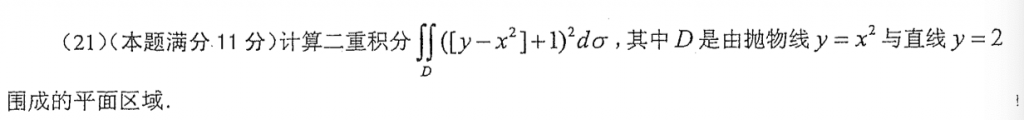
答案的方法我没看明白。。直接硬算的,不过最后的结果和答案也不一样,但是我感觉我算的好像没太大问题,等之后有空再算算看。

这个题也难的,第一问证明那个我感觉有些抽象,想了好久还是没整出来,答案的方法中用了一步反证法,挺好的手法,积累一下。第二问好像就是个公共解的问题,但是感觉也有点抽象,公共解同解这块有空还是需要回顾一下,李正元上讲的挺通透的。

基础题,通过$A^{*}$的特征值和特征向量实际上就可以把$A$的特征值和特征向量弄出来了,然后求A的话,还是我之前说的那个初等变换的方法比较好用,传送门:https://www.vsbf.fun/archives/2661,最后一题。
复盘结束,可能好久没做超越,一直在做真题或者错题啥的,所以刚上手的时候感觉状态都有些不对(这才几天?!),粗心错误出了好多,之后还是得多做一些高难度高质量的模拟题来提升手感,我去年年底大概十来天好像都没怎么碰那些比较难的卷子,做了李四这种卷子考了不少分就感觉自己稳了,所以最后爆炸,所以23的xdm到考前一天都要保持做题状态,不然前期的努力都功亏一篑着实不太划算。
码字较快,如果有错误欢迎评论区留言,感谢阅读!







Comments NOTHING