时间序列分析（上）——数据处理

时间序列也称为动态序列，是指将某种现象的指标数值按照时间顺序排列而成的数值序列。时间序列分析大致可分成三大部分，分别是描述过去、分析规律和预测未来，本篇文章将主要介绍时间序列分析中常用的三种模型：季节分解、指数平滑和ARIMA模型。

时间序列的基本概念

首先是时间序列数据：对同一对象在不同时间连续观察所取得的数据，例如：从出生到现在，你的体重数据、中国历年来的GDP数据以及在某个地方每隔一个小时测得的温度数据。

时间序列：时间序列也称为动态序列，是指将某种现象的指标数值按照时间顺序排列而成的数值序列。时间序列主要由两个要素构成：第一个要素是时间要素，比如年、季度、月、周......第二个要素是数值要素，也就是上面说的时间序列数据。

时间序列根据时间和数值性质的不同，可以分成时期时间序列和时点时间序列，分表示一段时间和一个时间点。

区分时期序列和时间序列

从出生到现在，你的体重数据（每年生日称一次）
中国历年来的GDP数据
在某个地方每隔一个小时测得的温度数据。

其中1和3是时点时间序列，2是时期时间序列。时期数据有一个特点是：它的值可以累加，但是时点序列不可以加。

主要原因在于：时期序列中的观测值反映现象在一段时期内发展的总量，不同时期的观测值可以相加，相加的结果表明现象在更长一段时间内的活动总量，而时点序列中的观测值反映现象在某一瞬间上所达到的水平，不同时期的观测值不能相加，因为相加的结果没有意义。（灰色预测模型里面有一个累加的过程）

时间序列分解

因为时间序列是某个指标数值长期变化的数值表现，所以时间序列数据变化背后闭然蕴含着数值变换的规律性，这些规律性就是时间序列分析的切入点。

一般情况下，时间序列的数值变化有以下四种

长期变化趋势（T）
季节变动规律（S）
周期变动趋势(C)
不规则变动（随机扰动项）（I）

长期趋势(Secular trend,T)指的是统计指标在相当长的一段时间内，受到长期趋势影响因素的影响，表现出持续上升或持续下降的趋势，通常用字母T表示。例如，随着国家经济的发展，人均收入将逐渐提升；随着医学水平的提高，新生儿死亡率在不断下降。

季节趋势(Seasonal Variation,S)是指由于季节的转变使得指标数值发生周期性变动。这里的季节是广义的，一般以月、季、周为时间单位，不能以年作单位。例如雪糕和棉衣的销量都会随着季节气温的变化而周期变化；每年的长假（五一、十一、春节）都会引起出行人数的大量增加。

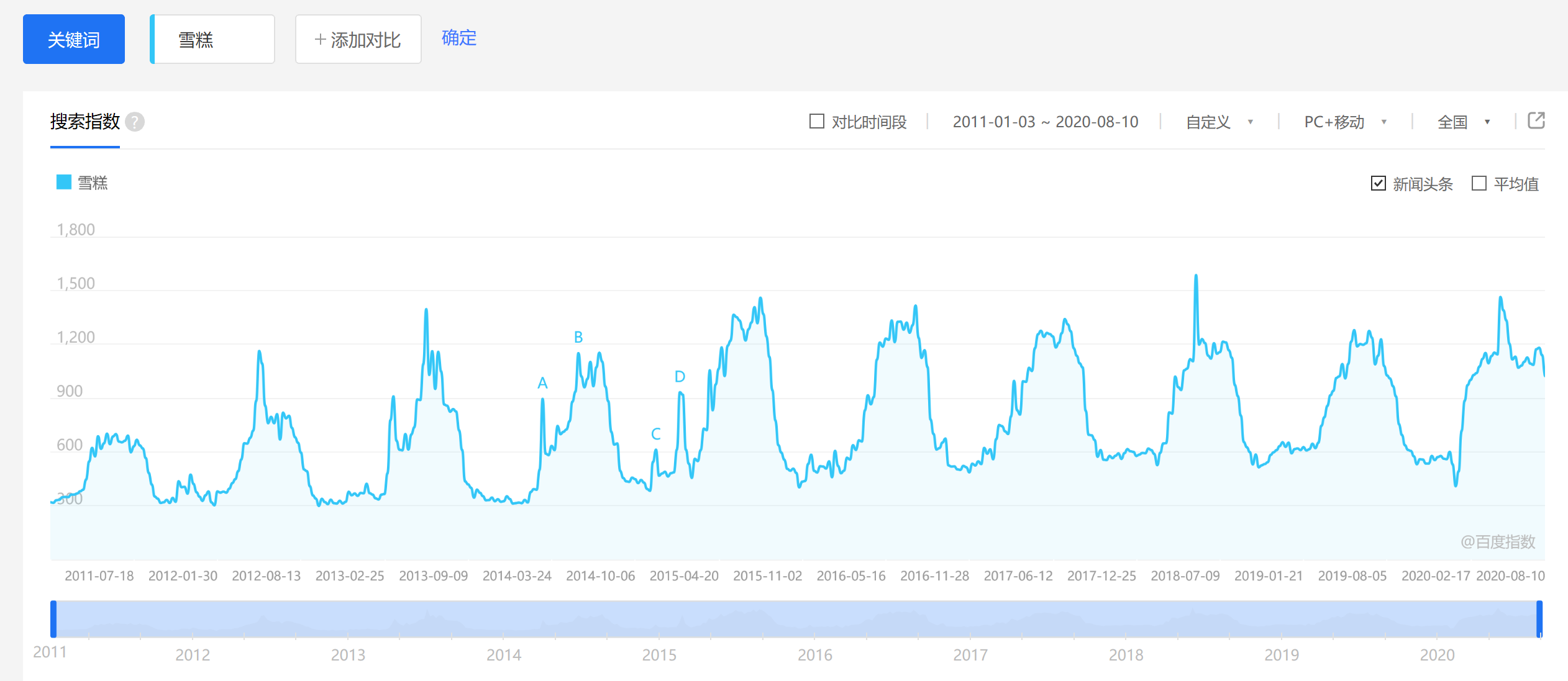
循环变动（CyclicalVariation,C）与季节变动的周期不同，循环变动通常以若干年为周期，在曲线图上表现为波浪式的周期变动。这种周期变动的特征变现为增加和减少交替出现，但是并不具严格规则的周期性连续变动。典型的周期案例就是市场经济的商业周期和的整个国家的经济周期。

不规则变动（IrregularVariation,I）是由某些随机因素导致的数值变化，这些因素的作用是不可预知和没有规律性的，可以视为由于众多偶然因素对时间序列造成的影响（在回归中又被称为扰动项）。

以上四种变动就是时间序列数值变化的分解结果。有时这些变动会同时出现在一个时间序列中，有时也可能只出现一种或计中，这是由引起各种变动的影响因素决定的，正式由于变动组合的不确定性，时间序列的数值变化才那么千变万化，这四种变动与指标数值最终变动的甚可能是叠加关系，也可能是乘积关系。

如果是相互独立的关系，那么应该是叠加模型：

$$
Y\,\,=\,\,T\,\,+\,\,C\,\,+\,\,S\,\,+\,\,I
$$

如果存在相互影响的关系，那么应该是乘积模型：

$$
Y\,\,=\,\,T\,\,\times \,\,C\,\,\times \,\,S\,\,\times \,\,I
$$

这里要注意：

数据具有周期性时才能使用时间序列分解，例如数据是月份数据(周期为12)、季度数据(周期为4) ，如果是年份数据则不行。
在具体的时间序列图上，如果随着时间的推移，序列的季节波动变得越来越大，则反映各种变动之间的关系发生变化，建议使用乘积模型；反之，如果时间序列图的波动保持恒定，则可以直接使用叠加模型；当然，如果不存在季节波动，则两种分解均可以。

使用SPSS快速进行数据预处理

SPSS处理时间序列中的缺失值

如果缺失值发生在时间序列的开头或者尾部，可以直接删除
如果发生在中间位置，则不能删除，删除后原有的时间可能会错位，可以采用替换缺失值的方法。

在spss中，使用如下操作，可以快速替换缺失值，选择转换 -> 替换确实值

然后开始替换

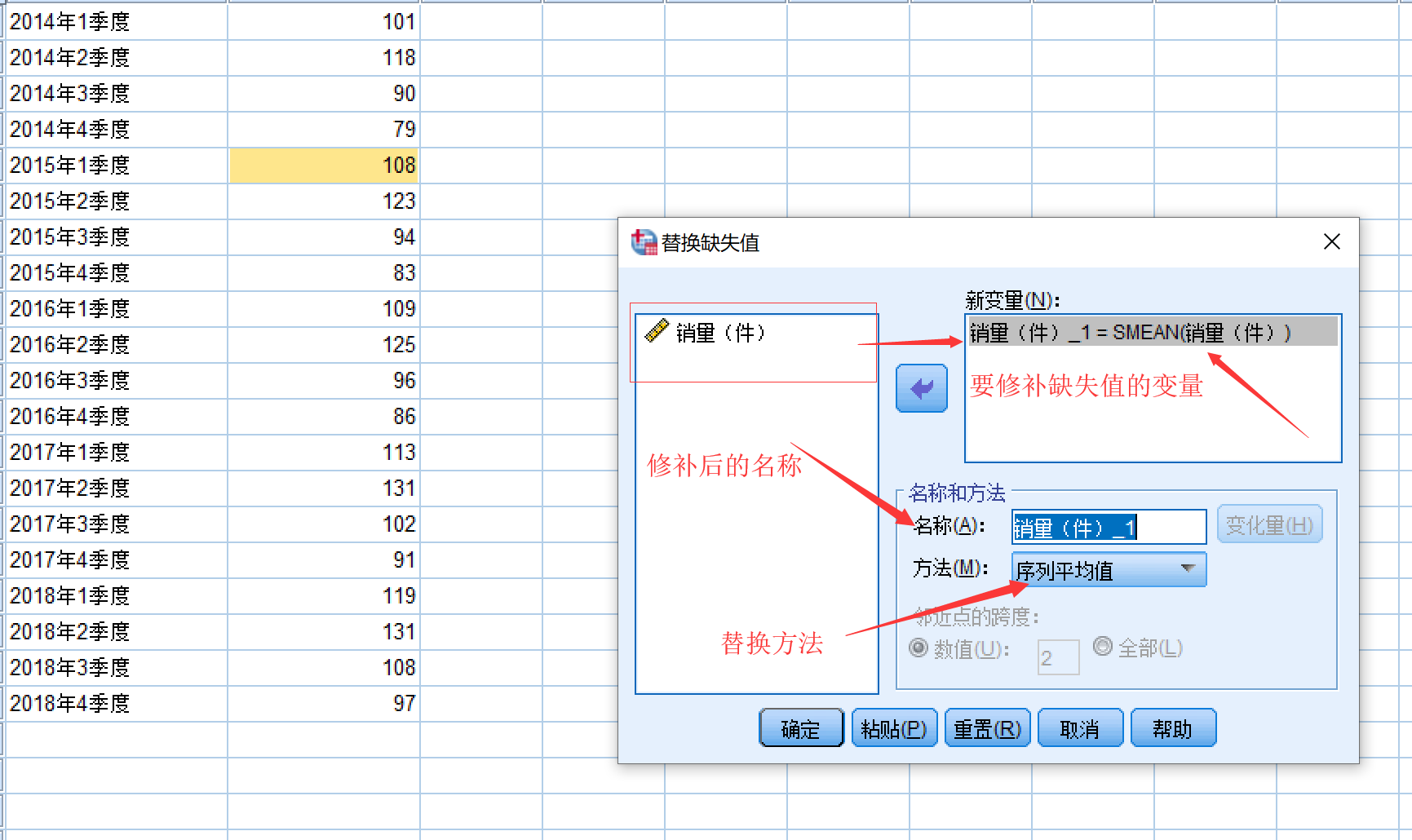
方法有五个：

序列平均值：用整个序列的平均数代替缺失值
临近点的平均值：用相邻若干个点的平均数来替换缺失值（默认为两个点）
临近点的中位数：用相邻若干个点的中位数来替换缺失值（默认为两个点）
线性插值：用相邻两个点的平均数来替换缺失值
临近点的线性趋势：将时期数作为x，时间序列值作为y进行回归，求缺失点的预测值

SPSS软件定义时间变量

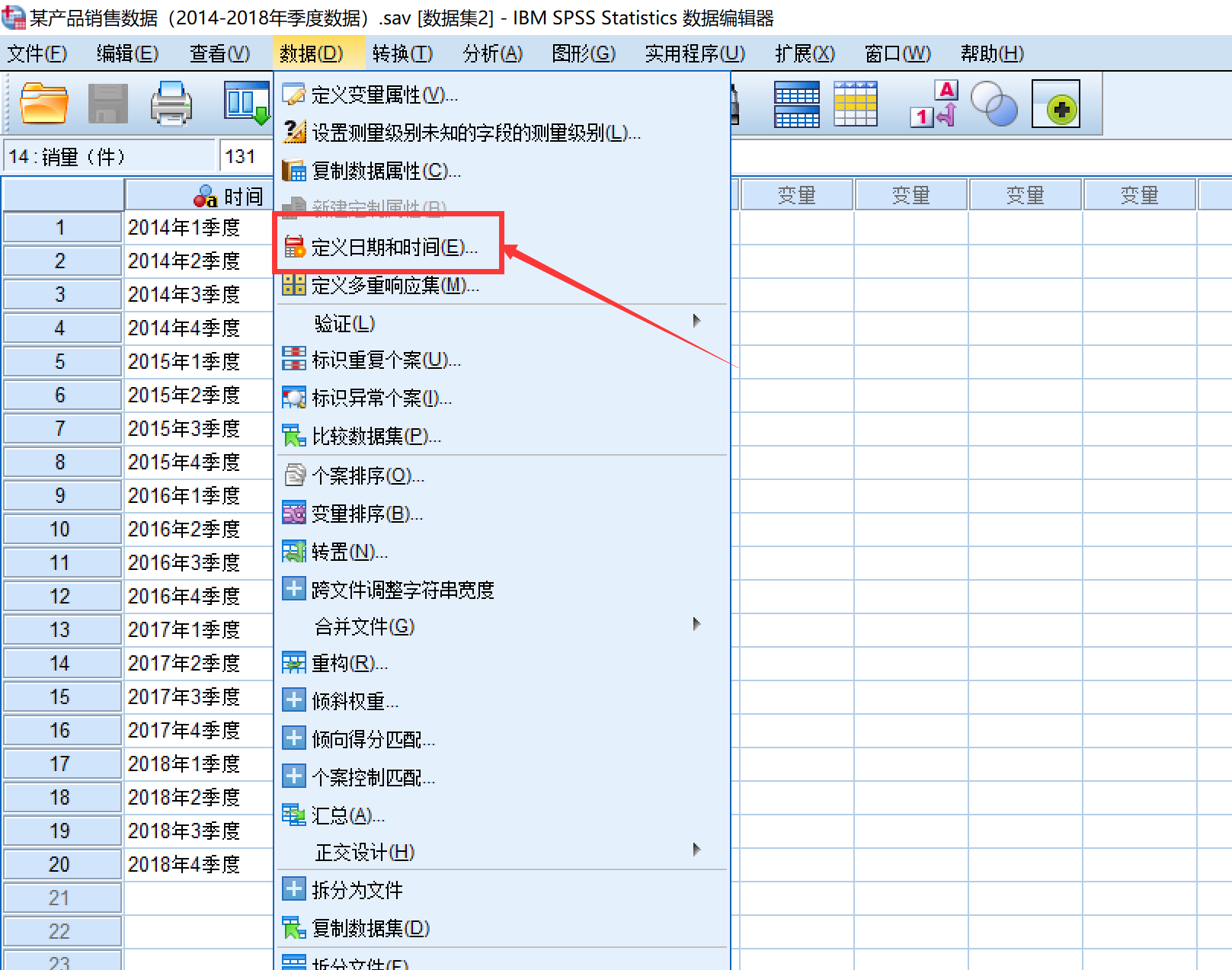
然后，选择合适的格式，并设置好起始时间

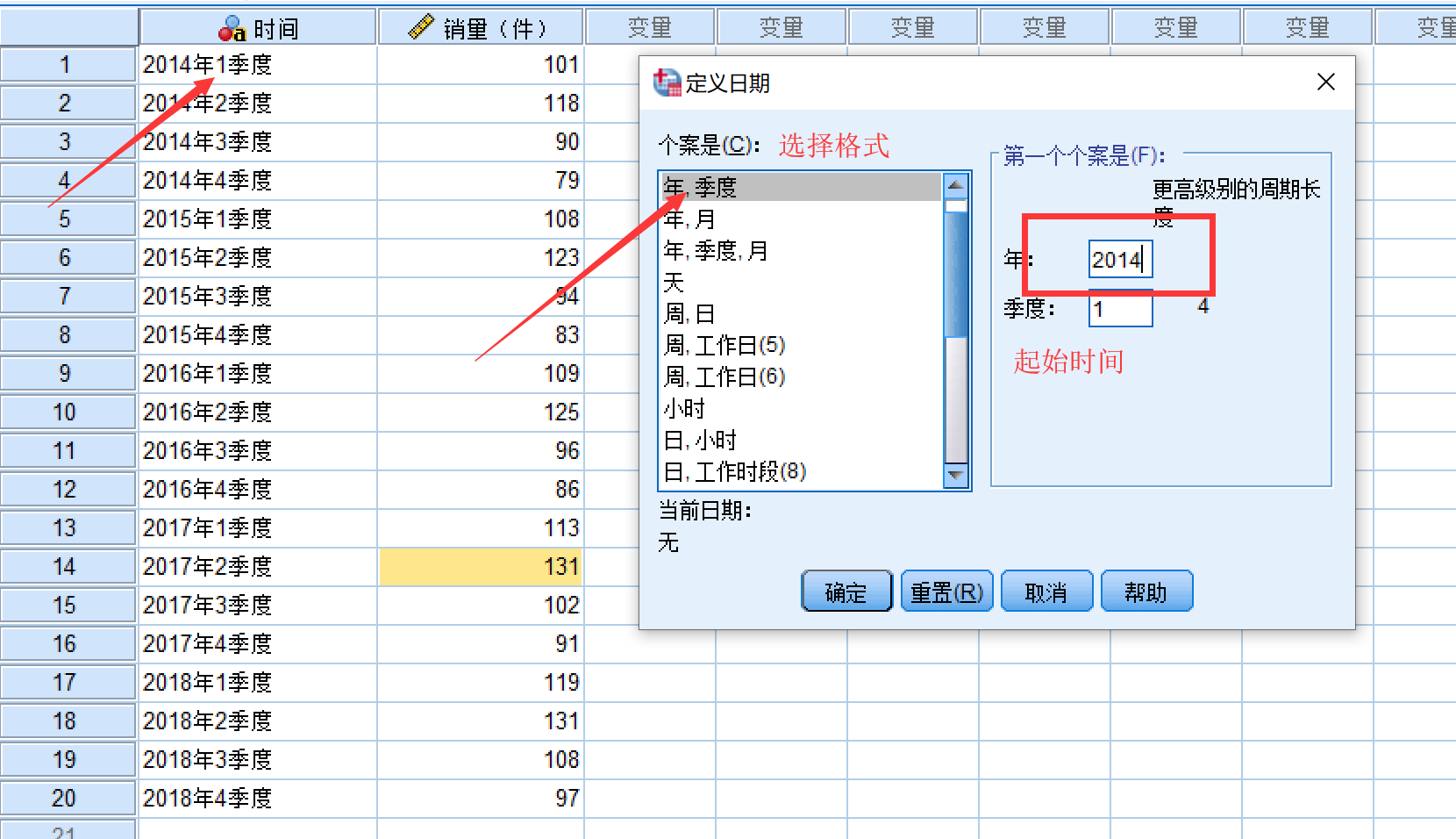
点击确定之后，就会生成变量：

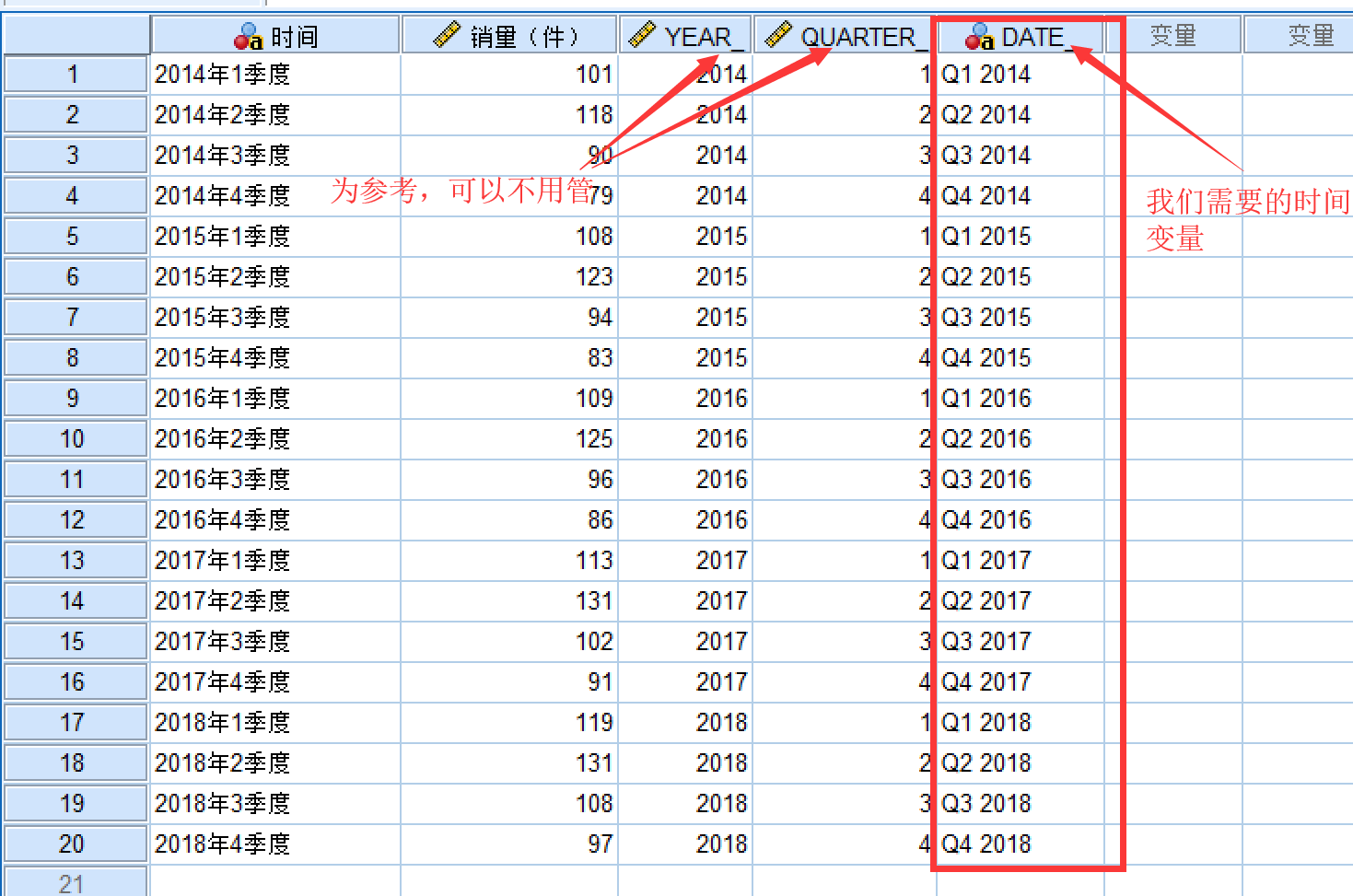
SPSS画出时间序列图

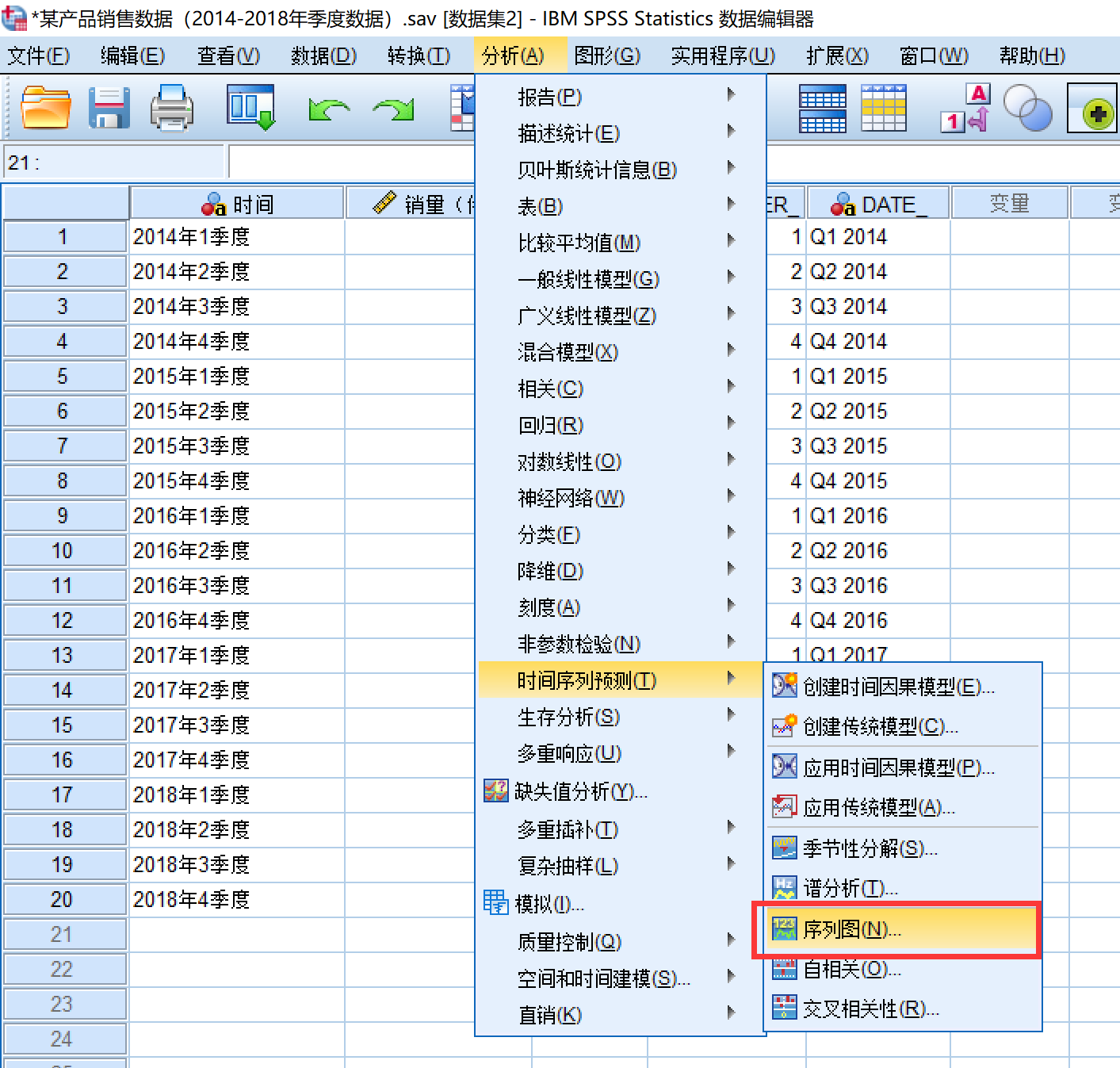
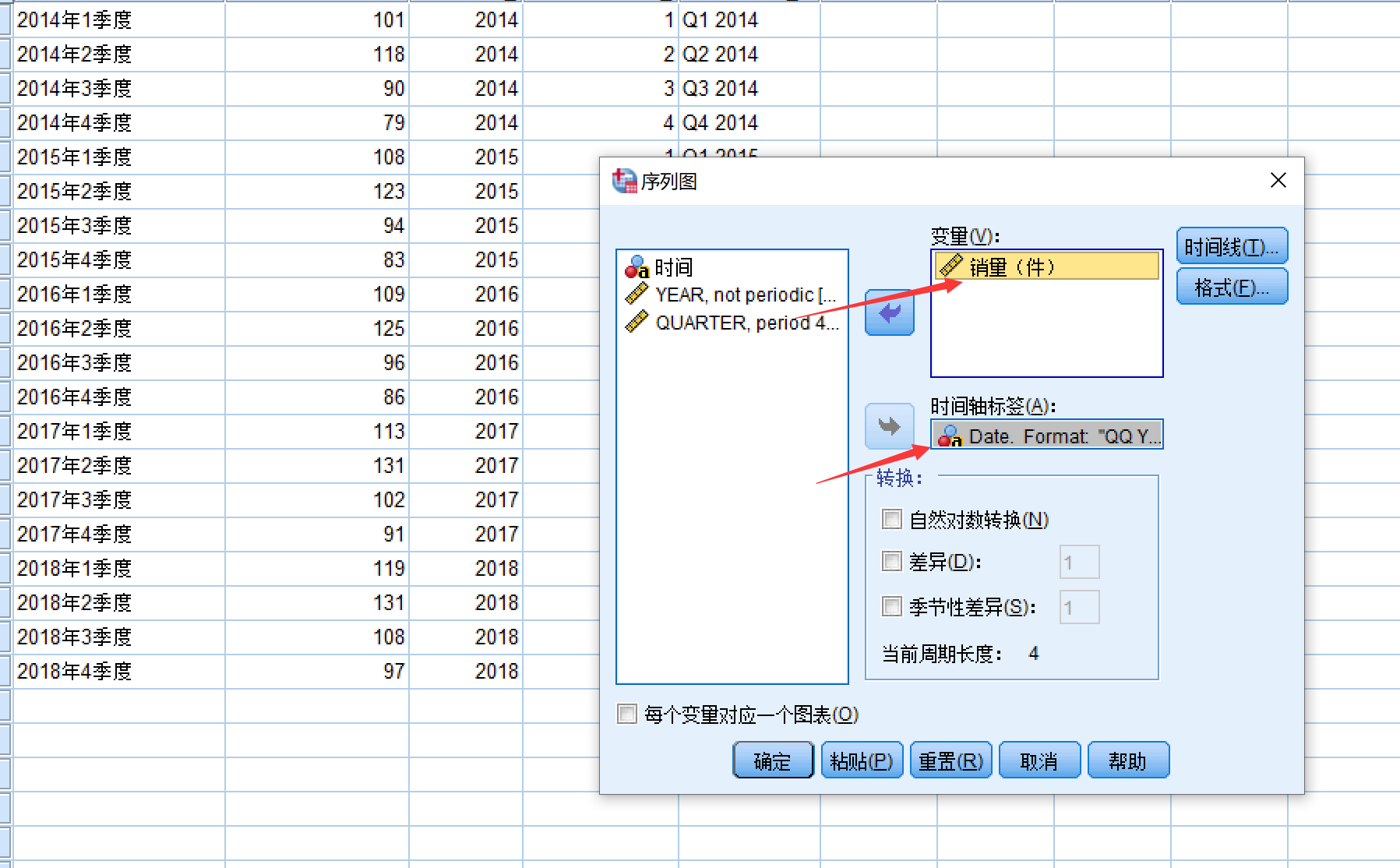
其他的地方也可以更改，看自己的需求，点击确定之后，就会生成时间序列图

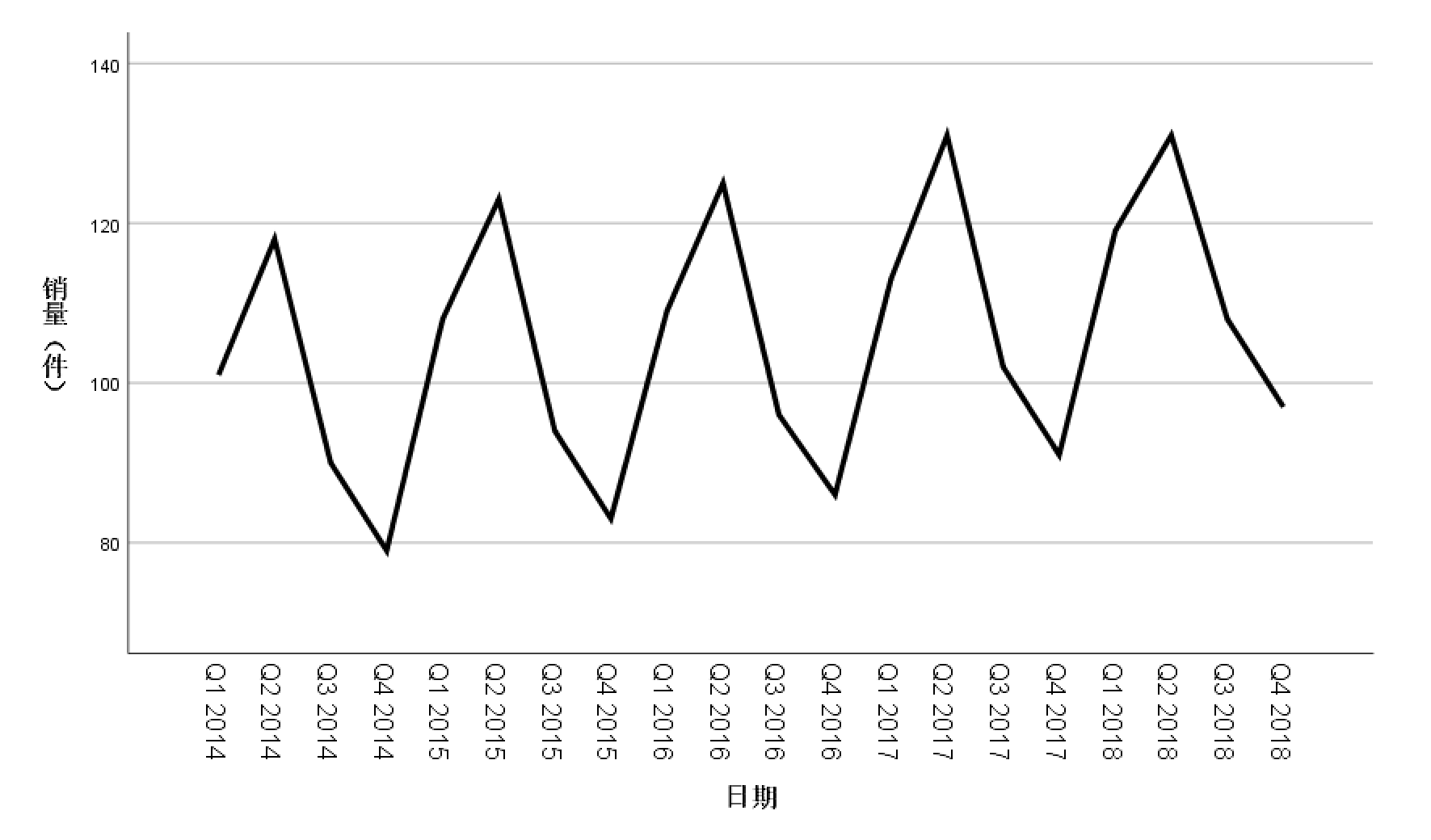
这张图可以放到论文中之后，一定要进行类似的解释：销量有向上的趋势，且第二季度的销量明显高于其他季度，因此数据表现出很强的季节性。随着时间变化，销量数据的季节波动变化不大，因此可使用加法分解模型。

SPSS进行季节性分解

首先找到季节性分解

在选择移动平均的时候，如果下面给的周期长度为奇数，选第一个，如果是偶数，选第二个

会弹出来一个框框，点击确定，然后spss会生成分解后的季节因子

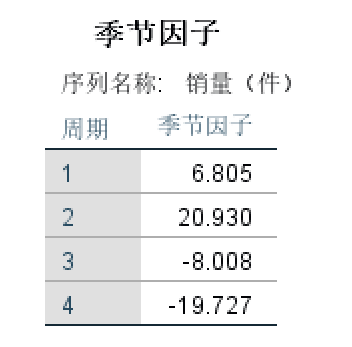
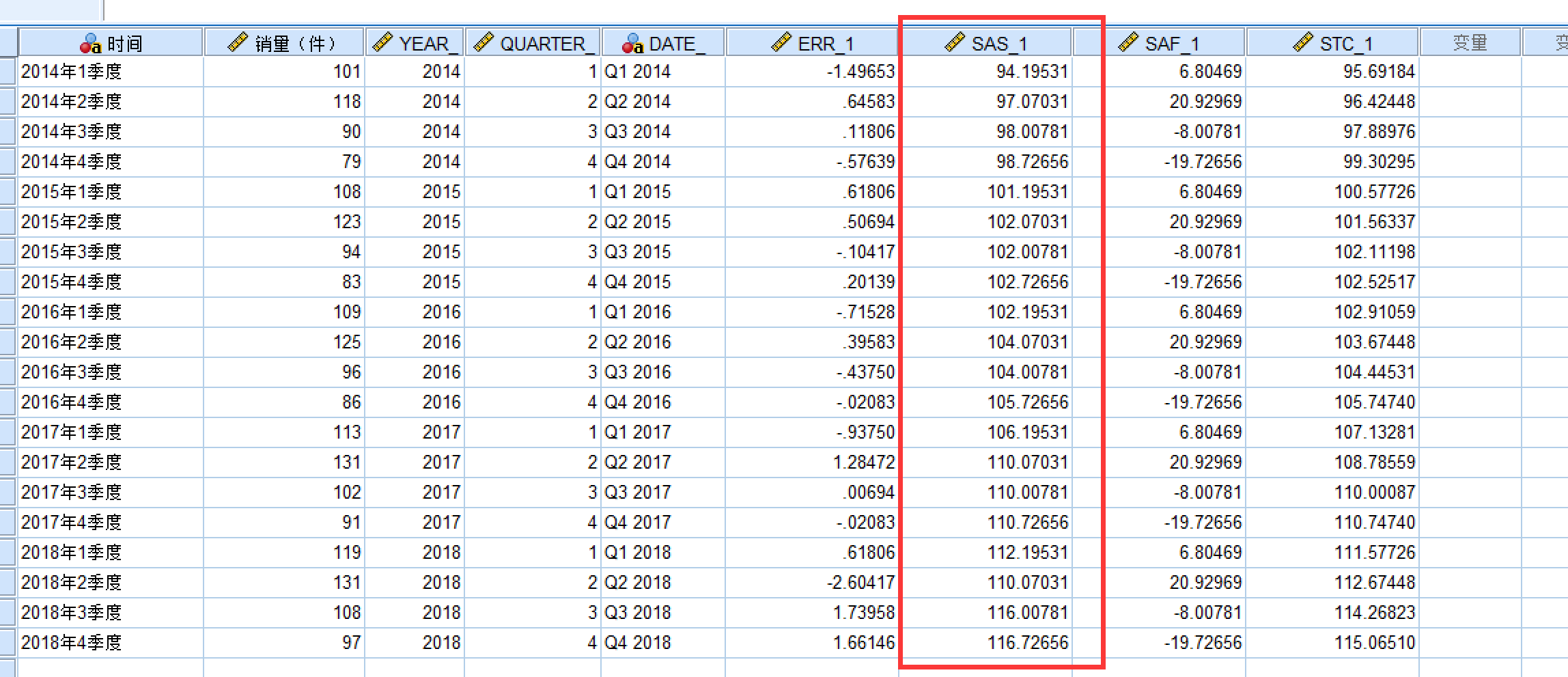
然后进行分析：从上表可知：第一二季度的季节因子为正，第三四季度的季节因子为负，这说明该品一二季度的平均销量要高于三四季度，且第二季度的平均销量要高于全年平均水平20.930件，第四季度的平均销量要低于全年平均水平19.727件（加法季节因子的和为0）

SPSS画出分解后的时序图

首先在变量窗口中，修改标签

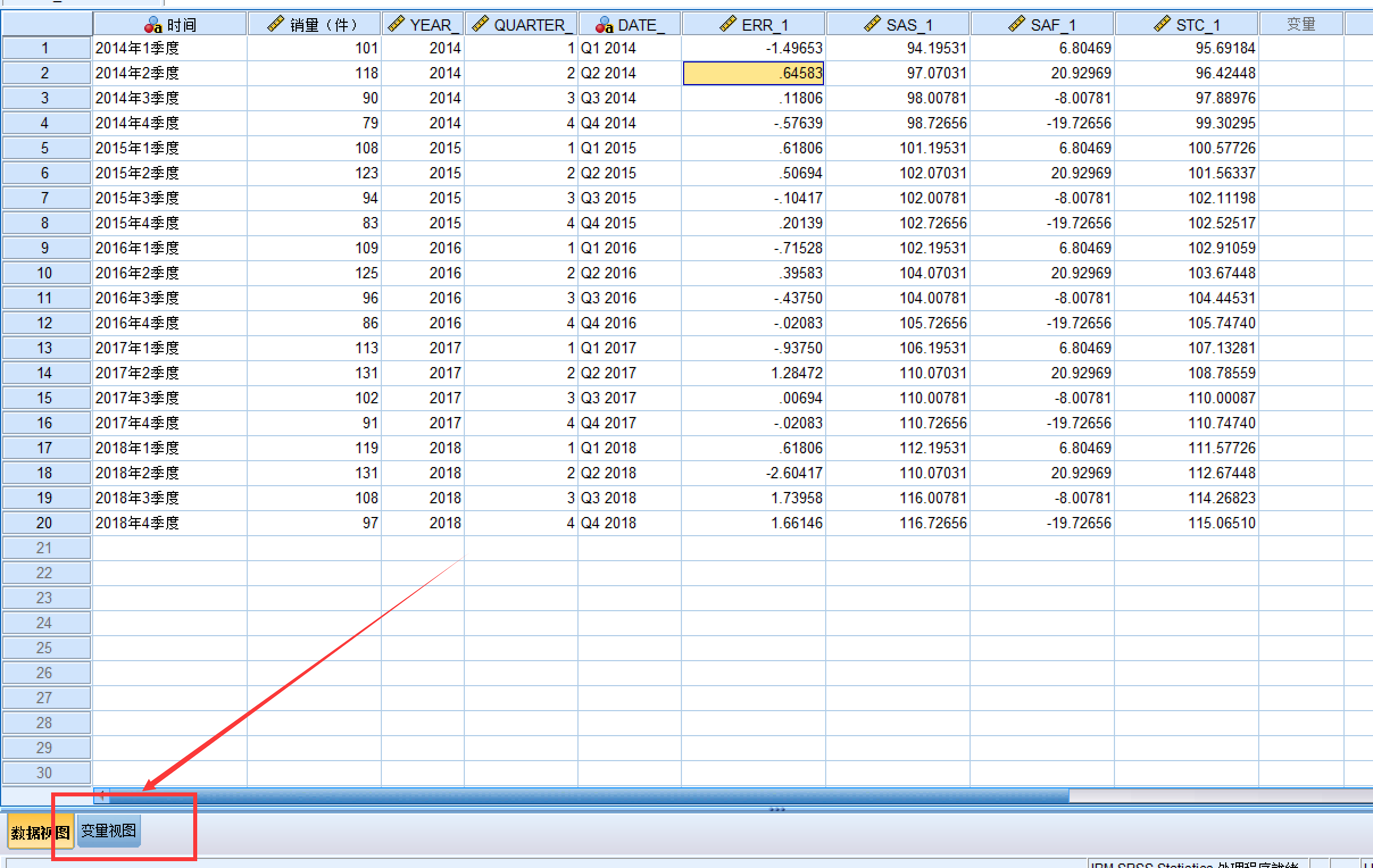
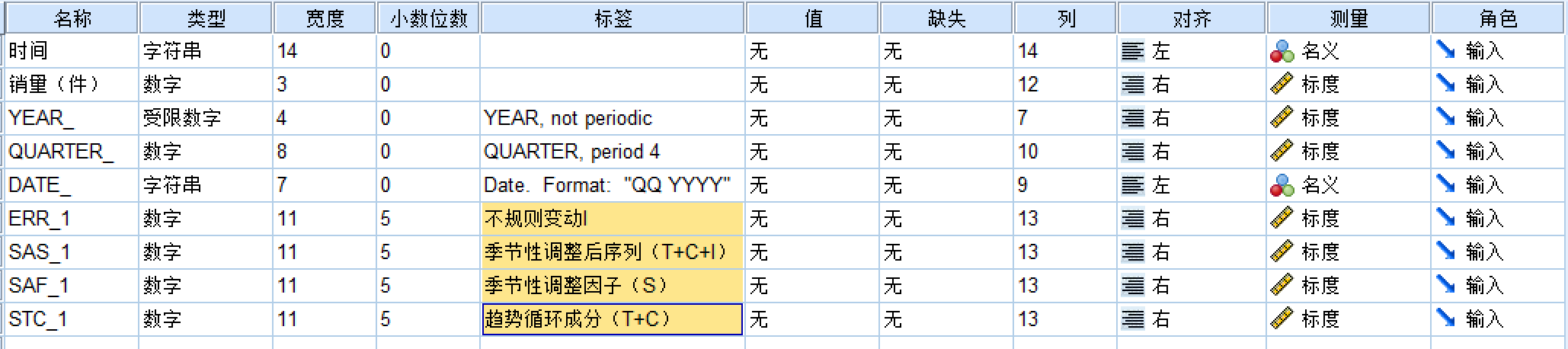
修改成这样的，然后画时序图，还是在分析-时间序列预测中找到时序图，然后加入变量，点击确定

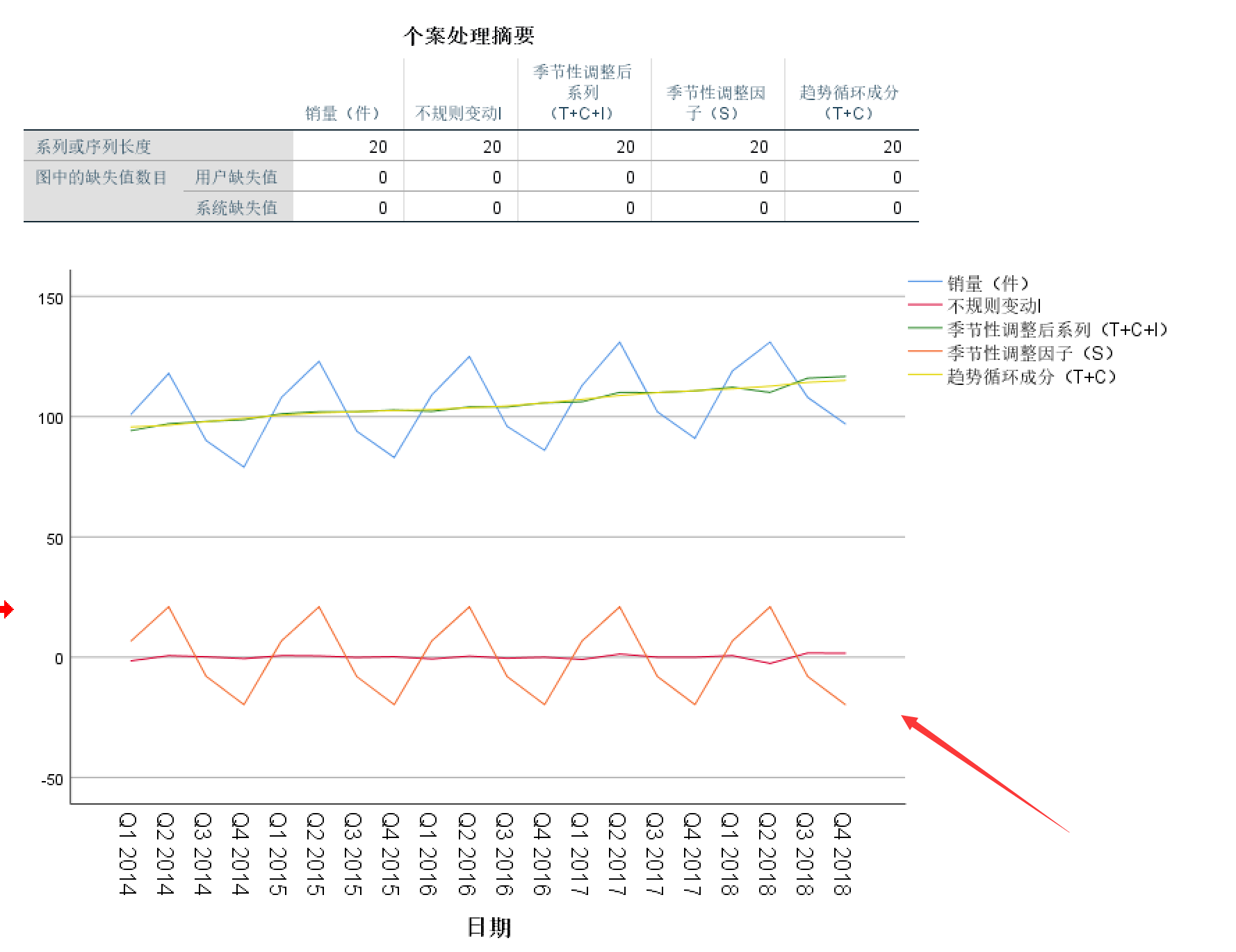
上面的就是我们需要的分解后的时序图了，分解出时序图之后，我们可以看到“季节调整后序列”（图上打错了...）和“循环趋势成分”这两条线比较平稳，为了方便，我们可以把季节性调整后序列（T+C+I）的数据取出来，然后放到matlab中进行拟合，将拟合出来的方程最后加上S，就得到了预测方程。当然这个预测方程肯定不够准确。所以我们就需要后面强大的时间序列模型。